توسع حل المعادلات والمتباينات اللوغاريتمية - رياضيات1-3 - ثالث ثانوي

-10 10 10 10 رابط الدرس الرقمي ם www.ien.edu.sa 5 y *118-1 توسع معمل الحاسبة البيانية : حل المعادلات والمتباينات اللوغاريتمية Solving Logarithmic Equations and Inqualites f1(x)=log (x) 10 0.5 -5 1.1 <-118-2 6.67 y 1.1 f2(x)=log (20 x+1) 3 -6.67 1- 2-6 لقد قمت بحل معادلات لوغاريتمية جبريًا، ويمكنك أيضًا حلها بيانيًا أو باستعمال جدول. فالحاسبة البيانية TInspire تحتوي على 10210 = y باعتباره أمرًا أساسيا. enter log ( x on VLO لعرض التمثيل البياني للدالة y = 10810 x ، اضغط على المفاتيح ويمكن أيضًا تمثيل الدوال اللوغارتمية بأساسات لا تساوي عشرة من دون استعمال صيغة تغيير الأساس، وذلك باستعمال أوامر مباشرة لكتابة الدالة اللوغاريتمية. نشاط 1 - استعمل الحاسبة البيانية TI-nspire؛ لحل المعادلة : 1 + log2 (6x – 8) = log (20x الخطوة 1 تمثيل طرفَي المعادلة بيانيا. مثل كل طرف بيانيًا على أنه دالة مستقلة. - أدخل (8 – log 6x ؛ لتكون f1، و 1 + log (20x لتكون f2 . ثم مثل المعادلتين بيانيا، وذلك بالضغط على المفاتيح: on ctrl 10x log2 (6x-8) enter tab f(x)-log (6-x-8) ctrl 10% log3 (20x+1) 2 118-3 1.1 6.67 y f2(x)=log (20-x+1) 6.67 fy 3 (4,4) 1 -6.67 f1(x)=10g (6-x-8) 2 *118-4 x f1(x).. ▼f2(x):... 1.1 log(6*x... log(20*x. f2(x)=log (20 x+1) 0. #ERR 0. 1f1(x)=10g 1. #ERR 2.77124 1012. 2. 3.38024 -6.67 3. 3.32193 3.74188 4. 4. 4. 51 15913 1 20086 10 enter الخطوة 2 استعمال ميزة نقاط التقاطع استعمل ميزة 4: نقاط التقاطع في " قائمة 6: تحليل الرسم البياني ، لتقدير إحداثي الزوج المرتب لنقطة تقاطع التمثيلين البيانيين. menu : واختر 6: تحليل الرسم البياني واختر منها 4 نقاط التقاطع اضغط على مفتاح ثم اضغط في أي نقطة على الشاشة وحرّك المؤشر مرورًا بنقطة التقاطع، سيظهر الزوج المرتب (4)، وحيث إن الإحداثي x لنقطة التقاطع يساوي 4 ؛ إذن حل المعادلة يساوي 4 الخطوة 3 : استعمل خاصية الجدول لتتحقق من الحلّ. من صحة حلك باستعمال خاصية الجدول وذلك بالضغط على مفتاح اثم اختيار تحقق 7 : الجدول 1 اظهار الجدول في شاشة جانبية (Ctrl + T) menu واختيار اختبر قيم الجدول لتجد قيمة x التي تتساوى عندها قيم y للتمثيلين البيانيين وهي 4 = x ، عند القيمة 4 = x ، تكون قيمتا y للدالتين متساويتين؛ لذا فإن حل المعادلة يساوي 4. تمارين استعمل الحاسبة البيانية Inspire لحل كل معادلة فيما يأتي، ثم تحقق من صحة حلك: log (7x + 1) = log (4x − 4) (2 log10 (1 = x) = log5 (2x+5) (4 log3 (3x — 5) = log3 (x+7) (6 log2 2x = log4 (x+3) (8 وزارة التعليم توسع - معمل الحاسبة البيانية حل المعادلات والمتباينات اللوغاريتمية 123 2024-1446 log2 (3x + 2) = log3 (12x + 3) (1 log2 3x = log3 (2x+2) (3 log4 (3x + 7) = log3 (5x-6) (5 - log5 (2x + 1) = log (3x − 2) (7

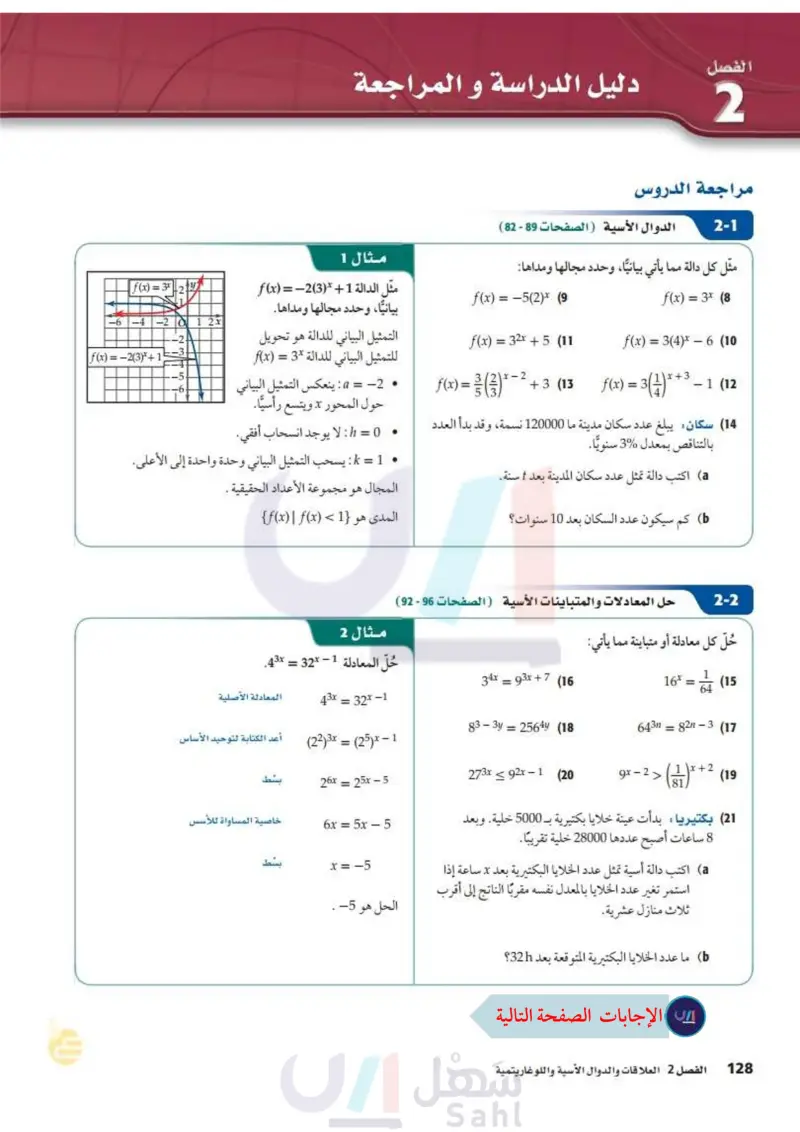
اعم 1 3 وبطريقة مشابهة، يمكنك استعمال الحاسبة البيانية TI -nspire لحل متباينات لوغاريتمية نشاط 2 استعمل الحاسبة البيانية Inspire الحل المتباينة اللوغاريتمية 10g4 (10x + 1) < 105 (16) + 6x . الخطوة 1 تمثيل المتباينات المناظرة أعد كتابة المسألة على صورة نظام من المتباينات. 6 المتباينة الأولى هي log (10) + (1) <y ، أو (1) + y > log 4 (10x، (y o 166x ، ثم مثلها بالضغط على المفاتيح: والمتباينة الثانية هي *119-1 1.1 y>log (10-x+1) 4 -1 0.2 y<log (16+6x) 5 -1 区 3 *119-1 1.1 y>log (10-x+1) (-0.121 7). 0.2 4 (1.5,2) y<log (16+6x) 5 -1 123456 y1 *119-1 y2 =log(10*x-=log(16+6* 1.1 1.79248 1.93729 1.2 1.85022 1.95357 1.3 1.90368 1.96944 1.4 1.95345 1.98491 1.5 2. 2. 6 اعد 2.01272 2.01474 5 وزارة التعليم Ministry of Education 2024-1446 1.2 1.1 A on del - > ctrl 10x log4 (10x — 1) - enter tab del < log5 (16+6x) enter menu الخطوة 2 : تحديد مجموعة الحل الحد الأيسر لمجموعة الحل هو عندما تكون المتباينة الأولى غير معروفة، وهي كذلك عندما 0 = 1 + 10x . 10x + 1 > 0 10 x ≤ -1 1 x ≤ 10 استعمل ميزة نقاط التقاطع لإيجاد الحد الأيمن، وذلك بالضغط على مفتا. 6 : تحليل الرسم البياني | ومنها 4 : نقاط التقاطع ثم اضغط في أي نقطة واختيار على الشاشة وحرّك المؤشر مرورًا بنقطة التقاطع، سيظهر الزوج المرتب (1.5) ويمكنك استنتاج أن مجموعة الحل هي {1.5 > x | −0.1 < x}. الخطوة 3: استعمال ميزة تطبيق القوائم وجداول البيانات للتحقق من الحل. ابدأ الجدول عند 0.1- ، واستعرض قيم x بزيادة 0.1 كل مرة ، وحرك المؤشر باحثًا في الجدول. اضغط على المفاتيح ) ، واكتب (1) Y1 = log 4 (10x في العمود الثاني، on في كل مرة، سترى أن قيم (6x + 108516 = 2 في العمود الثالث واختر الجدول تؤكد أن مجموعة حل المتباينة هي : {1.5 > x | -0.1 < x} . مرجع المتغير تمارين: استعمل الحاسبة البيانية TI-nspire؛ لحل كل متباينة مما يأتي، ثم تحقق من صحة حلّك: log 5 (12x + 5) ≤ log 5 (8x+9) (10 log 5 (3 - 2x) ≥ log5 (4x+1) (12 - log3 (3x — 5) ≥ log³ (x+7) (14 log₂ 2x ≤ log4 (x+3) (16 log 7 x < −1 (9 log 3 (7x – 6) < log 3(4x+9) (11 - log4 (9x + 1) > log3 (18x − 1) (13 log5 (2x + 1) < log (3x − 2) (15 - الفصل 2 العلاقات والدوال الأسية واللوغاريتمية 124

الفصل 2 دليل الدراسة و المراجعة ملخص الفصل المفاهيم الأساسية الدوال الأسية (الدرسان 2-1-12 • تكون الدوال الأسية على الصورة y = ab x ، حيث . a ± 0, b > 0 ,b # 1 • • خاصية المساواة للدوال الأسية: إذا كان 6 عددًا موجبا، حيث 1 b ، فإن b = by إذا وفقط إذا كان x = y . • خاصية التباين للدوال الأسية إذا كان 1 b، فإن bx > by إذا وفقط إذا كان x > y . • الدالة الأسية 1 ,f(x) = b دالة نمو أسي. المفردات الدالة الأسية ص 80 النمو الأسي ص 81 عامل النمو ص 82 الاضمحلال الأسي ص 82 عامل الاضمحلال ص 82 90 المعادلة الأسية ص الربح المركب ص 91 المتباينة الأسية ص 92 اللوغاريتم ص 95 . الدالة الأسية 1 , f ( x ) = b دالة اضمحلال أسي. اختبر مفرداتك اللوغاريتمات والدوال اللوغاريتمية (الدرس (3-2) إذا كان 10 < x , فإن الصورة الأسية للمعادلة اللوغاريتمية y = log x هي by = x ، والصورة اللوغاريتمية للمعادلة الأسية x = by هي 10gb x = y خصائص اللوغاريتمات الدرس 24 • خاصية المساواة للدوال اللوغاريتمية إذا كان 6 عددًا موجبا حيث 1 b ، فإن 4 108 = log x إذا وفقط إذا كان b . x = y • الضرب والقسمة : إذا كانت x y b أعدادًا حقيقية موجبة حيث 1 b فإن: y, log₁xy = log₁ x + log by log x - log by g log by x = الدالة اللوغاريتمية ص 97 المعادلة اللوغاريتمية ص 110 المتباينة اللوغاريتمية ص 112 اللوغاريتم العشري ص 116 صيغة تغيير الأساس ص 119 اختر المفردة المناسبة من القائمة أعلاه لإكمال كل جملة فيما يأتي: (1) الدالة التي على الصورة f(x) = b ، حيث 1 < b تسمى دالة (2) في المعادلة x = by . المتغير لا يسمى . للأساس 6 . (3) يسمى اللوغاريتم ذو الأساس 10 (4 X هي معادلة يظهر فيها المتغير على صورة أس. كتابة عبارات لوغاريتمية لوغاريتم القوة: لأي عدد حقيقي m، وأي عددين موجبين x,b حيث 1 فإن : 10gb x = m log x . • خاصية التباين للدوال اللوغاريتمية: إذا كان 1 ، فإن x 108b y إذا وفقط إذا كان x y . اللوغاريتم العشري (الدرس (2) • اللوغاريتم العشري هو اللوغاريتم الذي أساسه 10 . • صيغة تغيير الأساس: loga n = log b n_logba (5) يمكنك باستعمال مكافئة للوغاريتم بأساس مختلف. (6) يُسمى الأساس r - 1 في الدالة الأسية (1 - 1)A(t) = a (7) تُسمى الدالة y = log x ، حيث 1 + b > 0, b وزارة التعليم الفصل 2 دليل الدراسة والمراجعة 125 2024-1446

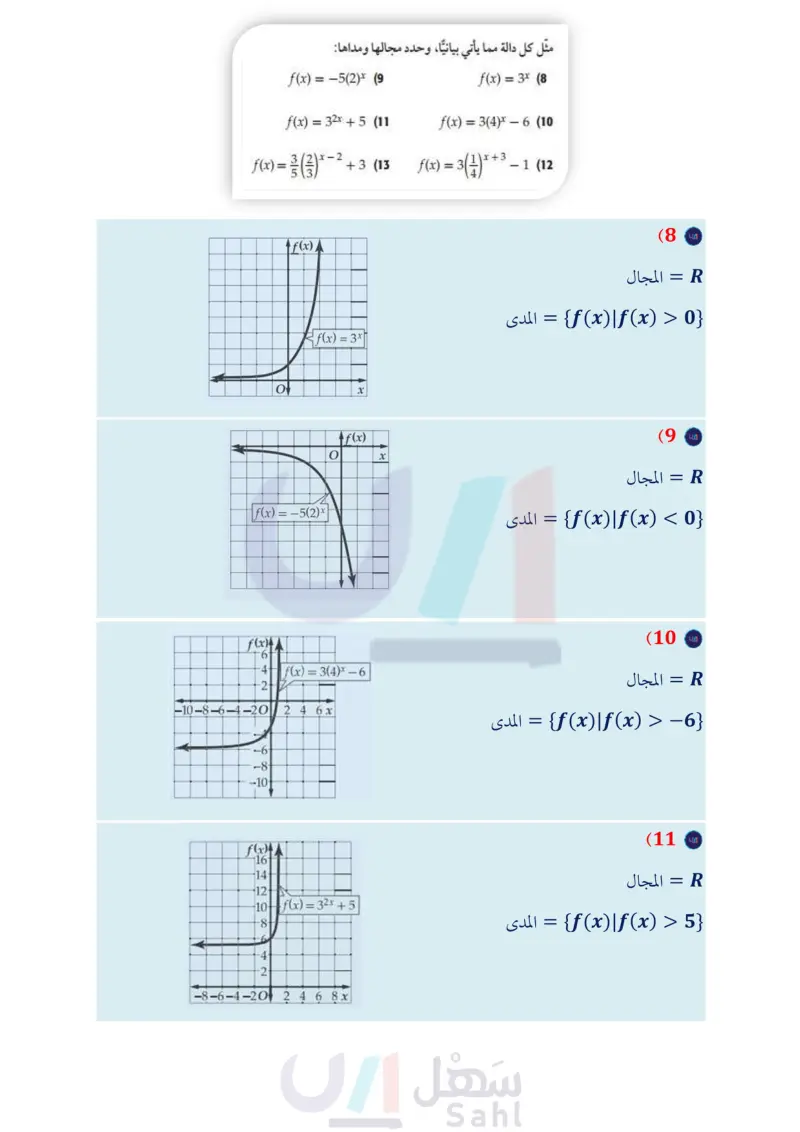
الفصل 2 دليل الدراسة و المراجعة مراجعة الدروس 2-1 الدوال الأسية الصفحات 80 - 87 ) مثل كل دالة مما يأتي بيانيًا، وحدد مجالها ومداها: f(x) = −5(2)* (9 f(x) = 3x (8 f(x) = 3(4)x - 6 (10 + 3 (13 f(x) = 3(1) * + 3 x+3 - 1 (12 f(x) = 32x + 5 (11 f(x) = 3 (3) - 2 3/2x- 5 (14) سكان يبلغ عدد سكان مدينة ما 120000 نسمة، وقد بدأ العدد بالتناقص بمعدل 3% سنويًّا. (a) اكتب دالة تمثل عدد سكان المدينة بعد أ سنة. كم سيكون عدد السكان بعد 10 سنوات؟ مثال 1 مثل الدالة 11 + f(x) = -2(3)x بيانيا، وحدد مجالها ومداها. التمثيل البياني للدالة هو تحويل للتمثيل البياني للدالة *3 = (f(x • 2 = a : ينعكس التمثيل البياني حول المحور x ويتسع رأسياً. Y:h=0 • 0 = h: لا يوجد انسحاب أفقي. f(x)=3x-2 -4-212x -2 |f(x) = −2(3)*+1 -3 23 +50 -5 -6. • 1 = : يسحب التمثيل البياني وحدة واحدة إلى الأعلى. المجال هو مجموعة الأعداد الحقيقية . المدى هو {1 > (f(x) | f(x} 2-2 حل المعادلات والمتباينات الأسية ( الصفحات 90- 94) مثال 2 حلّ كل معادلة أو متباينة مما يأتي: حل المعادلة 1 - 43x = 32x. 1 16% = 64 (15 34x = 93x + 7 (16 43x = 32x -1 83-3y=2564y (18 643n = 82n- (17 (22)3x = (25)x - 1 273x < 92x - 1 26x = 25x - 5 (20 9x-2 91 −2> (1)² 1 x + 2 81 (19 32x-1 المعادلة الأصلية أعد الكتابة لتوحيد الأساس بسط 21 بكتيريا : بدأت عينة خلايا بكتيرية بـ 5000 خلية. وبعد 8 ساعات أصبح عددها 28000 خلية تقريبًا. اكتب دالة أسية تمثل عدد الخلايا البكتيرية بعد x ساعة إذا استمر تغير عدد الخلايا بالمعدل نفسه مقربًا الناتج إلى أقرب ثلاث منازل عشرية. ) ما عدد الخلايا البكتيرية المتوقعة بعد 32h؟ 126 الفصل 2 العلاقات والدوال الأسية واللوغاريتمية 6x = 5x - 5 x = -5 الحل هو 5 . خاصية المساواة للأسس بسط وزارة التعليم Ministry of Education 2024-1446

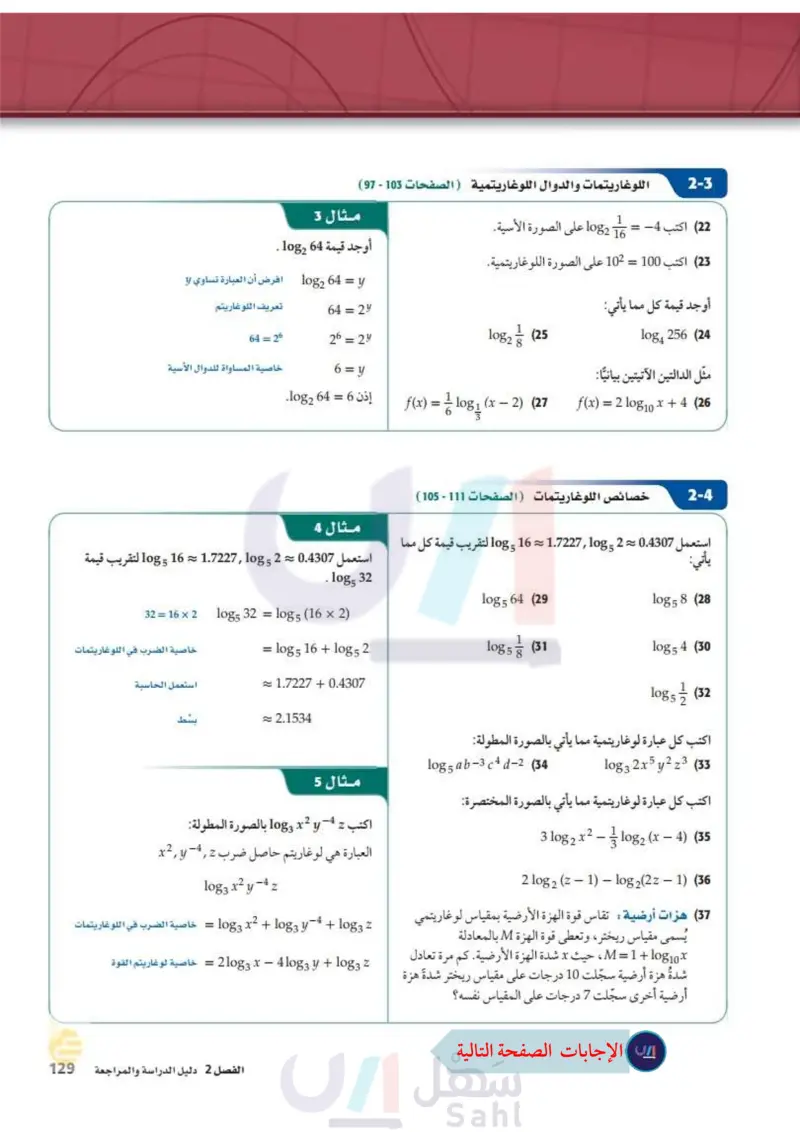
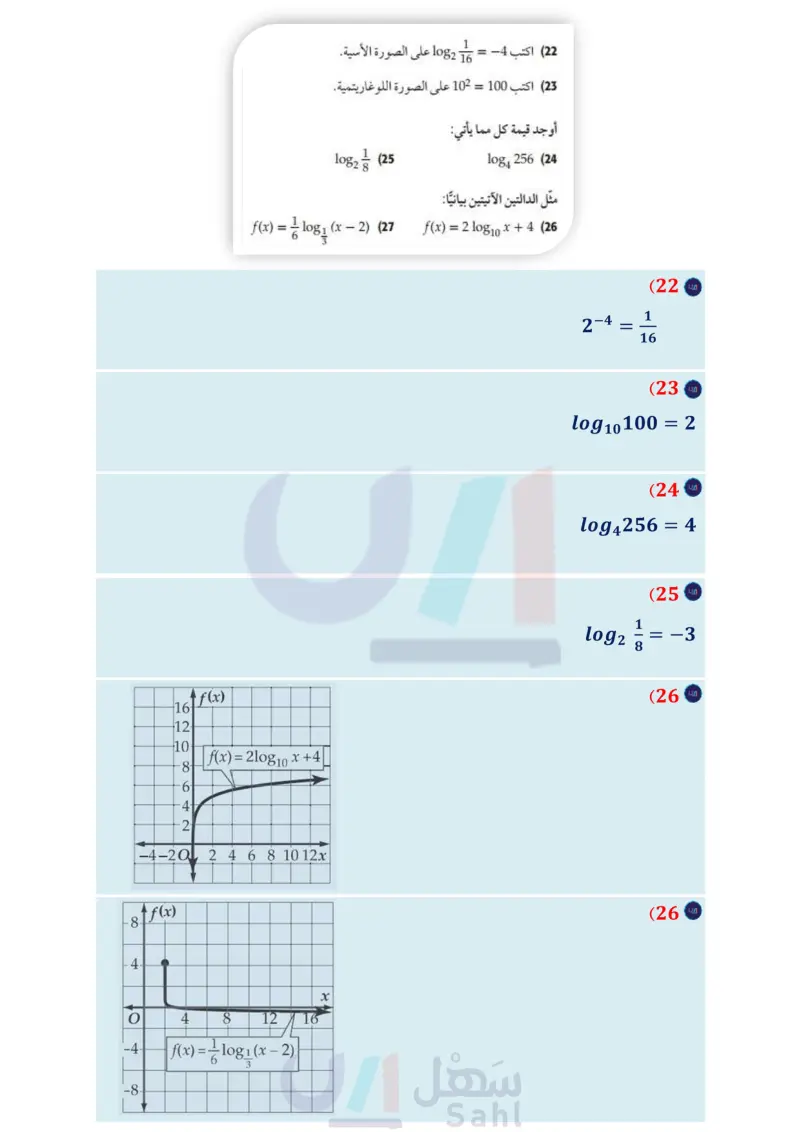
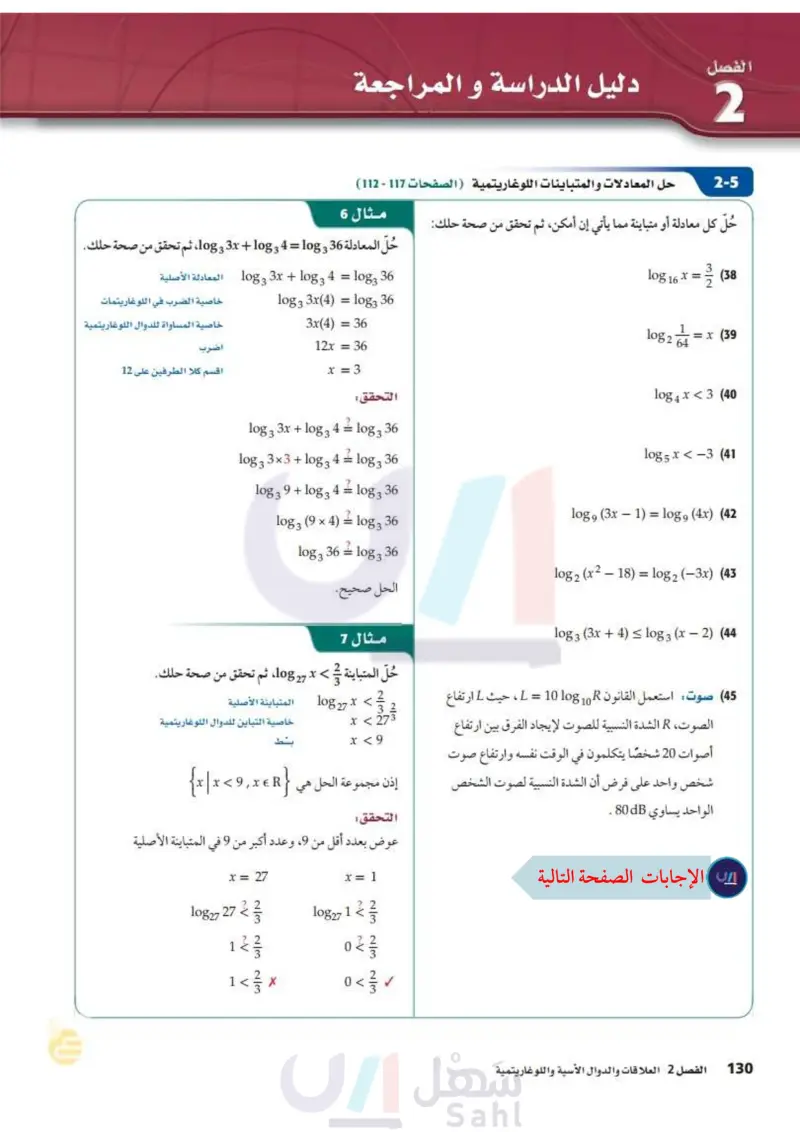
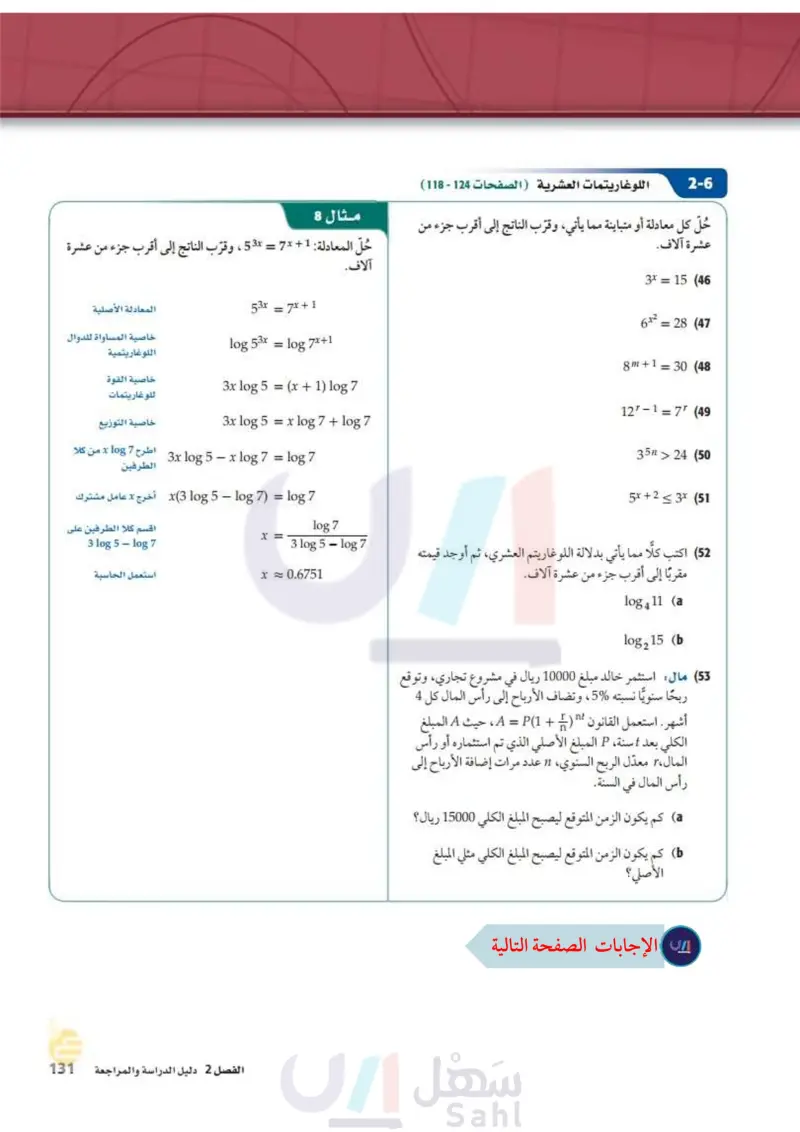
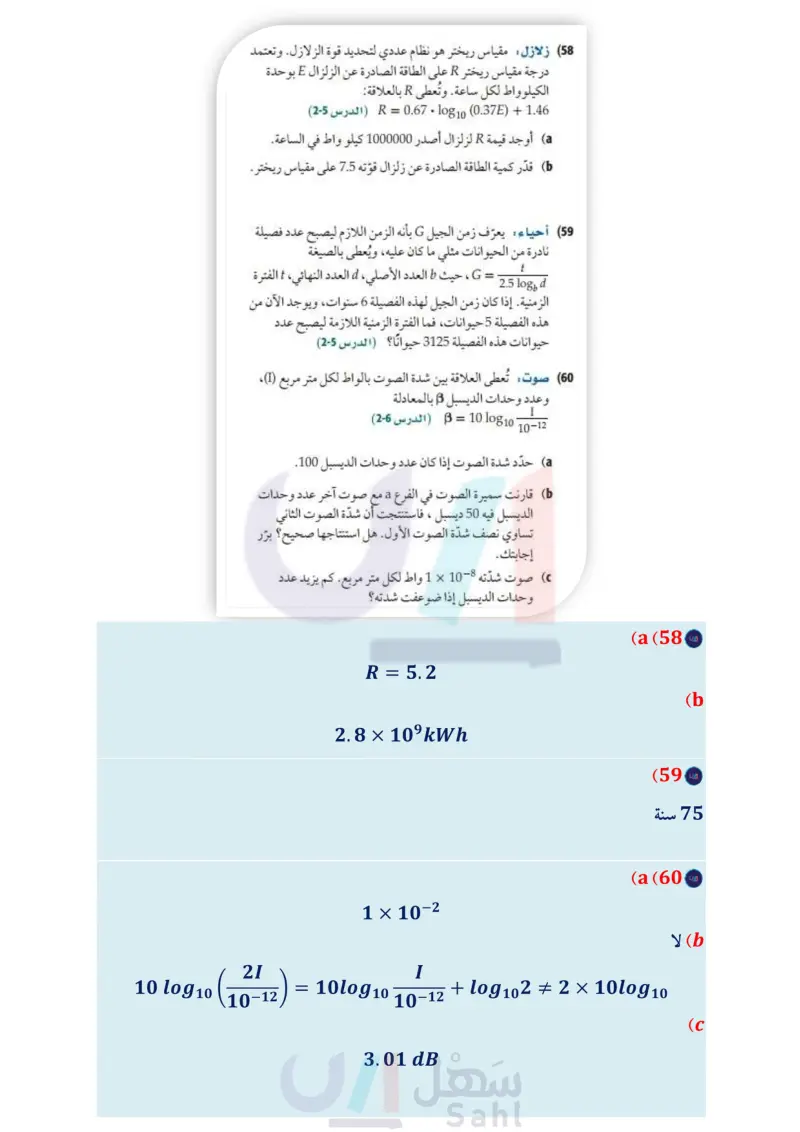
2-3 اللوغاريتمات والدوال اللوغاريتمية ( الصفحات 95 - 101 ) (22) اكتب 4- 1 =-45 16 1082 على الصورة الأسية. مثال 3 أوجد قيمة 64 1082 . (23) اكتب 100 = 102 على الصورة اللوغاريتمية. أوجد قيمة كل مما يأتي: y = 64 102 افرض أن العبارة تساوي y تعريف اللوغاريتم = 64 29 log2 64 = 26 26 = 29 1082 8 1 (25) log4 256 (24 خاصية المساواة للدوال الأسية إذن 6 = 64 log2. 6 = y مثل الدالتين الآتيتين بيانيا : f(x) = ½-½ log₁ (x − 2) (27 11083 – f(x) = = 2 log10 x +4 (26 2-4 خصائص اللوغاريتمات الصفحات 103 - 109 ) استعمل 0.4307 1.7227,182 ~ 16 10g لتقريب قيمة كل مما يأتي: مثال 4 استعمل 20.4307 2 5 1.7227,108 ~ 16 10g5 لتقريب قيمة .log5 32 log 564 (29 log 58 (28 32 = 16 × 2 1085 32 = 10g5 (16 × 2) خاصية الضرب في اللوغاريتمات استعمل الحاسبة = = log 5 16 + log 52 log 5 (31 log 54 (30 ≈ 1.7227 +0.4307 1 1085 3 (32) بسط ≈ 2.1534 اكتب كل عبارة لوغاريتمية مما يأتي بالصورة المطولة: log 1083 2x5y 223 (33) logs ab-3c4d-2 (34) اكتب كل عبارة لوغاريتمية مما يأتي بالصورة المختصرة: 2 3 log 2 x² - 1½ log2 (x − 4) (35 3 - 2 log 2 (z — 1) — log2(2z — 1) (36 مثال 5 اكتب 2 4 10g x y بالصورة المطولة: -4 y العبارة هي لوغاريتم حاصل ضرب x2,442 (37 هزات أرضية : تقاس قوة الهزة الأرضية بمقياس لوغاريتمي يُسمى مقياس ريختر وتعطى قوة الهزة M بالمعادلة و log3 x2 log3 x2y-4 2 log3 2 1083 + 4-10g3x2 + 10g3y = خاصية الضرب في اللوغاريتمات log10 x + 1 = ، حيث x شدة الهزة الأرضية. كم مرة تعادل 2 1083 + 210g3 x - 41083 y = خاصية لوغاريتم القوة شده هزة أرضية سجّلت 10 درجات على مقياس ريختر شدة هزة أرضية أخرى سجّلت 7 درجات على المقياس نفسه؟ وزارة التعليم الفصل 2 دليل الدراسة والمراجعة M127 2024-1446

دليل الدراسة و المراجعة الفصل 2 2-5 حل المعادلات والمتباينات اللوغاريتمية ( الصفحات 110 - 115 ) مثال 6 حلّ كل معادلة أو متباينة مما يأتي إن أمكن، ثم تحقق من صحة حلك: (38) 32 10816 x = 1 108264 = x (39 حل المعادلة 336 10g 3 3x + 10g 3 4 = 10g، ثم تحقق من صحة حلك . log3 3x + log3 4 = 108336 log 3 3x(4) = log3 36 3x(4) = 36 12x = 36 x = = 3 المعادلة الأصلية خاصية الضرب في اللوغاريتمات خاصية المساواة للدوال اللوغاريتمية اضرب اقسم كلا الطرفين على 12 وزارة التعليم Ministry of Education 2024-1446 التحقق : log log ? 10g3 3x + 10g3 4 = 108336 log log 10g33×3 + 10g3 4 = 108336 ? log log 39+ log 3 4 = log 3 ? 36 ? log 3 (9 × 4) = log 3 36 ? log 3 36 = log 3 36 الحل صحيح. مثال 7 حل المتباينة > x 10827، ثم تحقق من صحة حلك. log4 x <3 (40 log 5 x <3 (41 log9 (3x-1) = log, (4x) (42 log 2 (x²-18) = log 2 (−3x) (43 log 3 (3x+4) ≤ log 3 (x-2) (44 45 صوت استعمل القانون 1010810 = L ، حيث L الصوت، R الشدة النسبية للصوت لإيجاد الفرق بين ارتفاع أصوات 20 شخصًا يتكلمون في الوقت نفسه وارتفاع صوت شخص واحد على فرض أن الشدة النسبية لصوت الشخص الواحد يساوي 80dB . 2 10827 x < 3 2 x<27 x < 9 إذن مجموعة الحل هي التحقق : المتباينة الأصلية خاصية التباين للدوال اللوغاريتمية بسط {x|x<9,xeR} عوض بعدد أقل من 9 وعدد أكبر من 9 في المتباينة الأصلية x = 27 10827 27 22 123 1 < 23 23 23 X x x = 1 2 log27 1 } // 0 ~.V 3 0 < √ √ الفصل 2 العلاقات والدوال الأسية واللوغاريتمية 128

2-6 اللوغاريتمات العشرية ( الصفحات 116 - 122 ) مثال 8 حُلّ كل معادلة أو متباينة مما يأتي وقرب الناتج إلى أقرب جزء من عشرة آلاف. حل المعادلة : 1 + 53x = 7x ، وقرب الناتج إلى أقرب جزء من عشرة آلاف. 53x = 7x + 1 log 53x = log 7x+1 3x log 5 = (x + 1) log 7 3x log 5 x log 7 + log 7 8 3x = 15 (46 612 = 28 (47 gm + 1 = 30 (48) 127 - 1 = 77 (49) 35n > 24 (50 5x+2<3* (51 (52) اكتب كلا مما يأتي بدلالة اللوغاريتم العشري، ثم أوجد قيمته مقربًا إلى أقرب جزء من عشرة آلاف. log4 11 (a log 215 (b (53) مال استثمر خالد مبلغ 10000 ريال في مشروع تجاري، وتوقع ربحًا سنويًّا نسبته 5 ، وتضاف الأرباح إلى رأس المال كل 4 6 nt أشهر. استعمل القانون (1) = A، حيث المبلغ الكلي بعد ا سنة P المبلغ الأصلي الذي تم استثماره أو رأس المال، معدّل الربح السنوي، 1 عدد مرات إضافة الأرباح إلى رأس المال في السنة. كم يكون الزمن المتوقع ليصبح المبلغ الكلي 15000 ريال؟ كم يكون الزمن المتوقع ليصبح المبلغ الكلي مثلي المبلغ الأصلي؟ المعادلة الأصلية خاصية المساواة للدوال اللوغاريتمية خاصية القوة للوغاريتمات خاصية التوزيع log الطرفين 7 x 10g 5 - x 10g7 = log اطرح 1087 x من كلا log 3x log 7 xg - g 7) = log أخرج x عامل مشترك اقسم : كلا الطرفين على log 7 x = 3 log 5 - log 7 3 log 5 - log 7 استعمل الحاسبة x ~ 0.6751 وزارة التعليم الفصل 2 دليل الدراسة والمراجعة Ed 129 2024-1446

الفصل 2 دليل الدراسة و المراجعة تطبيقات ومسائل (54) أسعار تزداد أسعار السلع سنويًّا؛ بسبب ما يسمى التضخم. ونتيجة 58 زلازل مقیاس ریختر هو نظام عددي لتحديد قوة الزلازل. وتعتمد درجة مقياس ريختر R على الطاقة الصادرة عن الزلزال E بوحدة الكيلوواط لكل ساعة. وتُعطى R بالعلاقة: لذلك، يزداد سعر إحدى السلع بمعدل %4.5% سنويًّا، ويُعطى سعر هذه السلعة بالدالة (1.045) 275=(t) ، حيث t عدد السنوات بعد عام 1432هـ (الدرس (213) a) a كم كان سعر السلعة عام 1432هـ ؟ إذا استمر تضخم سعر السلعة بمعدل %4.5% سنويا، فكم سيكون سعرها عام 1447هـ تقريبًا ؟ (55) سيارات ينخفض سعر سيارة جديدة سنويًّا بدءًا من لحظة شرائها، ويُعطى سعر هذه السيارة بعد سنة من شرائها بالمعادلة 4 (0.8)80000 = (t) (الدرس (2-2) a ما معدل انخفاض سعر السيارة سنويًّا ؟ ) متى يصبح سعر السيارة مساويًا لنصف سعرها الأصلي؟ (56) استثمار ورثت فاطمة عن والدها مبلغ 250000 ريال، واستثمرته في مشروع، وتزايد كما في الجدول أدناه: (الدرس (2-2) السنة المبلغ (ريال) 1422 هـ 1430 هـ 1435 هـ 250000 329202 390989 a اكتب دالة أسية يمكن استعمالها لإيجاد المبلغ الكلي بعد سنة من الاستثمار. إذا استمر تزايد المبلغ بالمعدل نفسه، ففي أي سنة الكلي 500000 ريال تقريباً ؟ يصبح المبلغ 1.46 + (R= 0.67 • log10 (0.37E الدرس (25) أوجد قيمة R لزلزال أصدر 1000000 كيلو واط في الساعة. قدّر كمية الطاقة الصادرة عن زلزال قوته 7.5 على مقياس ريختر. (59) أحياء يعرّف زمن الجيل G بأنه الزمن اللازم ليصبح عدد فصيلة نادرة من الحيوانات مثلي ما كان عليه، ويُعطى بالصيغة =G، حيث العدد الأصلي، d العدد النهائي، t الفترة t 2.5 log d الزمنية. إذا كان زمن الجيل لهذه الفصيلة 6 سنوات، ويوجد الآن من هذه الفصيلة 5 حيوانات فما الفترة الزمنية اللازمة ليصبح عدد حيوانات هذه الفصيلة 3125 حيوانا؟ (الدرس 5-2) (60 صوت تُعطى العلاقة بين شدة الصوت بالواط لكل متر مربع (I)، وعدد وحدات الديسبل B بالمعادلة 1010810 = 3 ( الدرس 6-2 I 10-12 a حدّد شدة الصوت إذا كان عدد وحدات الديسبل 100. قارنت سميرة الصوت في الفرع a مع صوت آخر عدد وحدات الديسبل فيه 50 ديسبل ، فاستنتجت أن شدة الصوت الثاني تساوي نصف شدة الصوت الأول. هل استنتاجها صحيح ؟ برّر إجابتك. صوت شدّته 8 - 10 × 1 واط لكل متر مربع. كم يزيد عدد وحدات الديسبل إذا ضوعفت شدته؟ (57) كيمياء : يُعطى عدد السنوات اللازمة لاضمحلال الكمية الأصلية (61) مال : السعر الأصلي لسلعة 8000 ريال، وازداد سعرها باستمرار؛ بسبب التضخم بطريقة الربح المركب حتى بلغ 12000 ريال بعد 5 No جرام من مادة مشعة لتصبح N جرام بالمعادلة N 16 log 10 No 1 108103 2 = الدرس (23) بشكل تقريبي، بعد كم سنة تقريبًا يضمحل 100g من المادة المشعة لتصبح 308؟ ما النسبة التقريبية لما يتبقى من 100g بعد 40 سنة؟ سنوات الدرس (26) إذا كان معدل التضخم %6% سنويًّا، فبعد كم سنة يصبح سعر السلعة 12000 ريال ؟ ما معدل التضخم الذي يصبح عنده سعر السلعة 12000 ريال بعد 5 سنوات؟ 130 الفصل 2 العلاقات والدوال الأسية واللوغاريتمية وزارة التعليم Ministry of Education 2024-1446

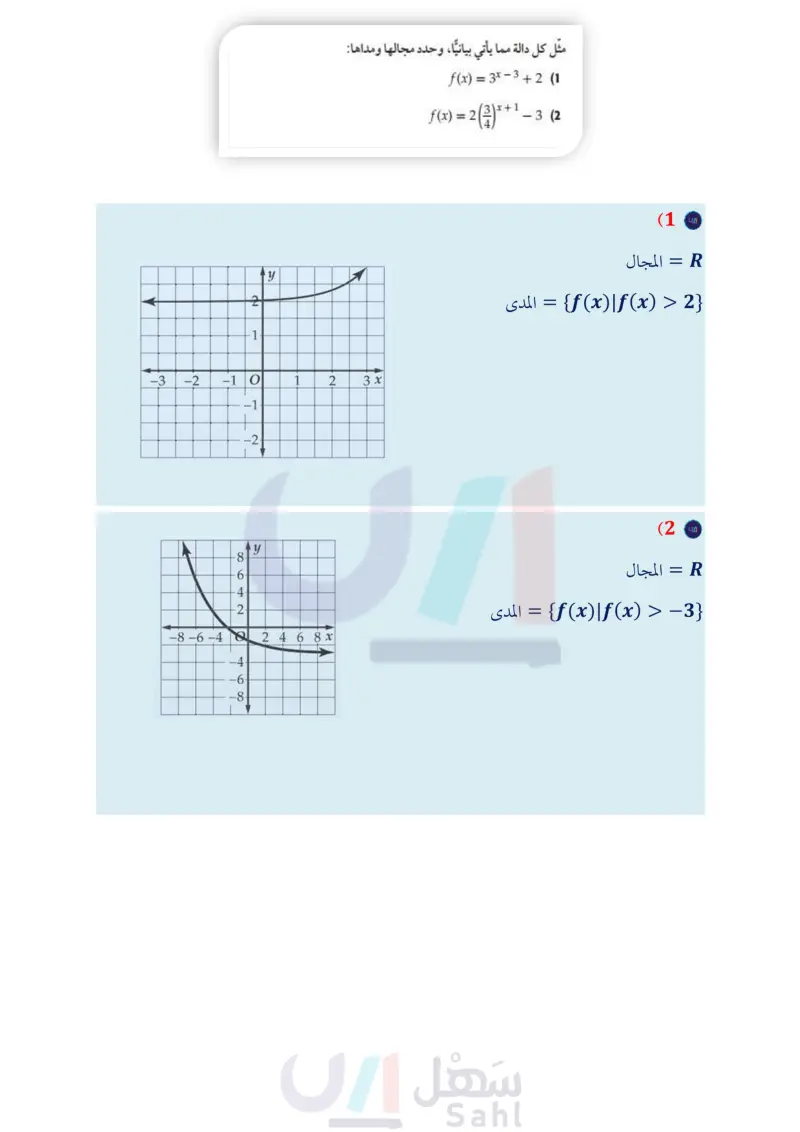
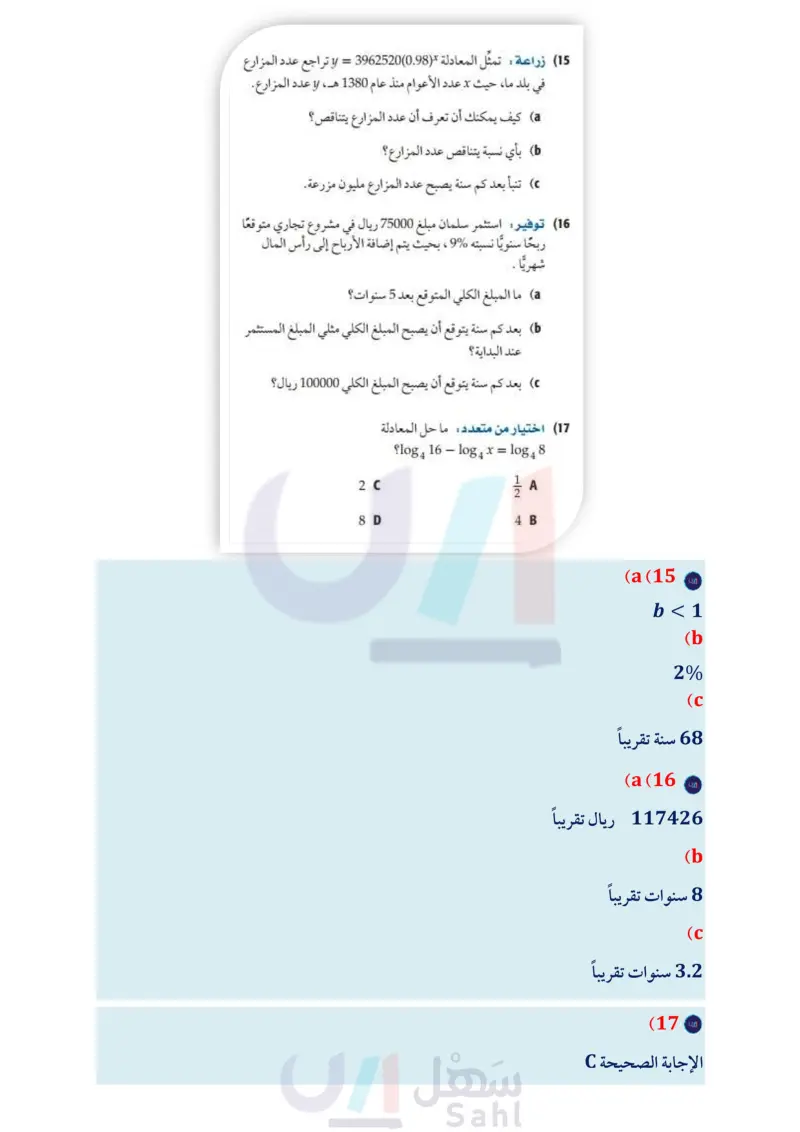
الفصل 2 اختبار الفصل مثل كل دالة مما يأتي بيانيًا، وحدد مجالها ومداها: f(x) = 3x – 3 + 2 (1 f(x) = 2 ()* — 3 (2) 3x + 1 حلّ كل معادلة أو متباينة مما يأتي وقرب الناتج إلى أقرب أربع منازل عشرية كلما لزم ذلك: (4 8c + 1 = 162 + 3 (3) 9x-2 27 x 2a+3 32a 1 (5 = log2 (x² = 7) = log2 6x (6 log5 x > 2 (7 1083 x + 1083 (x - 3 = 10g34 (8) 6n-1 ≤11" (9 استعمل 0.4307 102, 1.4899 ~ 11 1085، لتقريب قيمة كل مما يأتي إلى أقرب جزء من عشرة آلاف: (15) زراعة تمثل المعادلة (0.98)3962520 = y تراجع عدد المزارع في بلد ما، حيث x عدد الأعوام منذ عام 1380هـ ، y عدد المزارع. 6 a كيف يمكنك أن تعرف أن عدد المزارع يتناقص ؟ بأي نسبة يتناقص عدد المزارع؟ . تنبأ بعد كم سنة يصبح عدد المزارع مليون مزرعة. 16 توفير استثمر سلمان مبلغ 75000 ريال في مشروع تجاري متوقعًا ربحًا سنويًّا نسبته %9% ، بحيث يتم إضافة الأرباح إلى رأس المال شهريًا . 6 a ما المبلغ الكلي المتوقع بعد 5 سنوات؟ بعد كم سنة يتوقع أن يصبح المبلغ الكلي مثلي المبلغ المستثم عند البداية؟ بعد كم سنة يتوقع أن يصبح المبلغ الكلي 100000 ريال ؟ . (17) اختيار من متعدد: ما حل المعادلة 20 – log4 16 - log 4 x = log48 A 12 8 D 4 B log5 44 (10 1085 (11 (12) سكان كان عدد سكان مدينة ما قبل 10 أعوام 150000 نسمة، تزايد بعد ذلك عددهم بمعدل ثابت كل سنة، ليصبح الآن 185000 نسمة. اكتب دالة أسية يمكن أن تمثل عدد السكان بعد x سنة إذا استمرت الزيادة بالمعدل نفسه مقربًا الناتج إلى أقرب أربع منازل عشرية. كم يصبح عدد السكان بعد 25 سنة؟ 3 13) اكتب = = 27 1089 على الصورة الأسية. 1 (14) اختيار من متعدد ما قيمة 1084 64 18) اختيار من متعدد : أي الدوال الآتية لها التمثيل البياني أدناه؟ y 4 321 -4-20 1 2 3 4x y = log 10 (x-5) A y = 5 log 10 x B -2. -3 y = log10 (x + 5 y = -5 log10 x D (19) اكتب العبارة اللوغاريتمية x + 6 10g3 ( 2 - 2 + 10g3 t2 21083- بالصورة المختصرة. وزارة التعليم الفصل 2 اختبار الفصل M131 Edu 2024-1446 13 C 3 D 3A براحت B

(f• g)(x) = f(x) • g(x) ({})(x) = f(x) 8(x) 8(x) 0 nt A = P(1 + 7/7)" log₁ xy = log₁ x + log₁ y M = x1 + x2 y1+ y21 2 (a b)2 a22ab+b² ― = a2 b2 (a - b)(a + b) y الدالة الثابتة |f(x) = = C الدالة التكعيبية |f(x)=x³= YA وزارة التعليم Ministry of Education 2024-1446 العمليات على الدوال الضرب القسمة (f + g)(x) = f(x) + g(x) (f − g) (x) = f(x) − g(x) الدوال الأسية واللوغاريتمية الربح المركب خاصية الضرب في اللوغاريتمات logy xp = p log, x loga x logb x = loga b logb y = logb x - الهندسة الإحداثية نقطة المنتصف كثيرات الحدود مربع الفرق الفرق بين مربعين logby d = V (x2 - x12 + (y2 - 1)2 m = 92 - 91 x2-x1,x2x1 -b +Vb2 – 4ac x = ato 20 (a + b)2 = a2 + 2ab + b2 الصيغ الجمع الطرح خاصية لوغاريتم القوة صيغة تغيير الأساس خاصية القسمة في اللوغاريتمات المسافة الميل القانون العام مربع المجموع التمثيل البياني للدوال الرئيسة (الأم) X دالة القيمة المطلقة الدالة التربيعية = x2 = |x| الدالة المحايدة y = x v x X x x O x У = x 6 دالة المقلوب x #0 У x دالة أكبر عدد صحيح دالة الجذر التربيعي Ꭹ y = V x, x ≥ 0 | (0, 0) x f(x) = [x] y الصيغ والرموز X 132

8 f(x) = |x| f(x) = { f(x) = [[ x ]] f-1 logb x log x وزارة التعليم الصيغ والرموز E 133 2024-1446 مالانهاية سالب مالانهاية دالة القيمة المطلقة الدالة متعددة التعريف دالة أكبر عدد صحيح معكوس الدالة f لوغاريتم x للأساس b اللوغاريتم العشري R Q I N W N f(x) f(x) = { f(x) = |x| f(x) = [x] f(x,y) [fg](x) f-1(x) 1 bn b₁₁ = √b D R U B C J Q الرموز مجموعة الأعداد الحقيقية مجموعة الأعداد النسبية مجموعة الأعداد غير النسبية مجموعة الأعداد الصحيحة مجموعة الأعداد الكلية مجموعة الأعداد الطبيعية دالة f بمتغير x يساوي تقريبا الدالة المتعددة التعريف دالة القيمة المطلقة دالة أكبر عدد صحيح دالة بمتغيرين تركيب الدالتين أو 8 الدالة العكسية للدالة f الجذر النوني لـ b المجال المدى تقاطع اتحاد المجموعة الخالية