الدوال - رياضيات1-3 - ثالث ثانوي
الفصل الأول: تحليل الدوال
الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية
نشاط الفصل الأول: تحليل الدوال
نشاط الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية
1-1 الدوال Functions رابط الدرس الرقمي www.ien.edu.sa فيما سبق: ورموزها. (مهارة سابقة) لماذا ؟ درست مجموعات الأعداد تتضمن الكثير من الأحداث في حياتنا كميتين مرتبطتين معًا؛ فقيمة فاتورة الكهرباء مثلا تعتمد على كمية الاستهلاك؛ لذا يمكنك تخفيض قيمة فاتورة منزلكم والابتعاد عن الإسراف المنهي عنه بترشيد الاستهلاك. والآن : أصفُ مجموعات جزئية من مجموعة الأعداد الحقيقية. أتعرف الدوال، وأحسب قيمها، وأجد مجالاتها. المفردات: الصفة المميزة للمجموعة set-builder notation رمز الفترة interval notation الدالة function رمز الدالة الشركة السعودية للكهرباء المشترك أحمد نواف العبدالله العنوان القراية العالية | XIII SETEA قرابة مدة ٥٨٣٤٨ رقم المنطقة . Ri..... ارجو حرقية من الفاتورة من على البيكم رقم القوة ابتهال لطبقة تعريفية اوسط إدارة كهرباء مدينة الرياض رقم الفاتورة هاتف الطواري بداية الفترة موقع الشركة نهاية الفترة T-14-- +/- زيزي الشركة السعودية الكورية المالك بانه سيتم البدء بنطاب ضريبة القيمة محالة بمقر على الاستها وضع الرسوم ALKAHABA وصف مجموعات جزئية من مجموعة الأعداد الحقيقية : تستعمل الأعداد الحقيقية لوصف كميات مثل النقود، والزمن والمسافة، وتحتوي مجموعة الأعداد الحقيقية R على المجموعات الجزئية الآتية: مفهوم أساسي الأعداد الحقيقية الأعداد الحقيقية R الرمز المجموعة الأعداد غير النسبية الأعداد النسبية الأعداد الصحيحة الأعداد الكلية الأعداد الطبيعية I Z W Q N Z W N أمثلة T, √3 = 1.73205... 0.125, - 7_8, 2 = 3 0.666... -5,17,-23,8 0, 1, 2, 3... 1, 2, 3, 4... function notation المتغير المستقل independent variable المتغير التابع dependent variable الدالة المتعددة التعريف يمكنك وصف هذه المجموعات ومجموعات جزئية أخرى من الأعداد الحقيقية باستعمال الصفة المميزة للمجموعة؛ إذ تستعمل الصفة المميزة للمجموعة خصائص الأعداد ضمن المجموعة لتعريفها. ويقرأ الرمز ” | “ حيث، والرمز " ع " ينتمي إلى أو عنصر في . {x|-3≤x≤16, x Є Z} piecewise-defined function 8 الفصل 1 تحليل الدوال X ينتمي إلى مجموعة الأعداد المعطاة. لها هذه الخصائص ... الأعداد X حيث ... مثال 1 استعمال الصفة المميزة اكتب كلًا من مجموعات الأعداد الآتية باستعمال الصفة المميزة للمجموعة: {8, 9, 10, 11, ...} (a تتكون المجموعة من كل الأعداد الكلية الأكبر من أو تساوي 8. {x | x ≥ 8, x Є W} x<7 (b وتقرأ مجموعة الأعداد X ، حيث x أكبر من أو تساوي 8 ، و x تنتمي إلى مجموعة الأعداد الكلية. تتكون المجموعة من كل الأعداد الحقيقية التي تقل عن 7. {x | x < 7, x Є R} -2<x<7 (c تتكون المجموعة من كل الأعداد الحقيقية التي تزيد على 2- وتقل عن 7. {x | −2 < x <7, x = R} تحقق من فهمك -1 ≤ x ≤5 (1C x-3 (1B {1, 2, 3, 4, 5, ...) (1A وزارة التعليم Ministry of Education 2024-1446

الأعداد الحقيقية
استعمال الصفة المميزة
1A- اكتب كلا من محموعات الأعداد الآتية باستعمال الصفة المميزة للمجموعة:
أصف مجموعات جزئية من مجموعة الأعداد الحقيقية.
قراءة الرياضيات " تُستعمل رموز الفترات لوصف المجموعات الجزئية من مجموعة الأعداد الحقيقية، فيستعمل الرمزان ”[" أو "]“ للدلالة على انتماء طرف الفترة إليها، بينما يُستعمل الرمزان " ( “ أو ”) “ للدلالة على عدم انتماء طرف الفترة إليها. تسمى الفترة غير محدودة أما الرمزان ” أو ” فيُستعملان للدلالة على أن الفترة غير محدودة. ”a“ غير محدودة : إذا كانت قيمها تزداد أو تنقص دون حدود (دون و فترات محدودة فترات غير محدودة توقف) . . إرشادات للدراسة الرمزان ، يُقرأ الرمز ”“ (اتحاد)، ويعني: جميع العناصر المنتمية إلى كلا المجموعتين. يُقرأ الرمز ”“ (تقاطع)، ويعني: جميع العناصر المشتركة بين المجموعتين المتباينة رمز الفترة المتباينة رمز الفترة [a,∞) x ≥ a [a,b] a≤x≤b [10'00-) x ≤ a (a, b) a<x<b (a,∞) x > a [a, b) a<x<b (-∞, a) x<a (a,b] a<x<b مثال 2 استعمال رمز الفترة اكتب كلا من المجموعات الآتية باستعمال رمز الفترة: -8<x<16 (a x<11 (b ) 16- ≥ x أو 5 < x تحقق من فهمك -4 ≤ y < −1 (2A (-8, 16] (-0, 11) (-∞, -16] U (5,∞) a> 3 (2B o > x > 00 (00'00-) x < −2 ix > 9 (2C تمييز الدالة : تذكَّر أن العلاقة تذكَّر أن العلاقة هي قاعدة تربط عناصر مجموعة مثل A (المدخلات) مع عناصر من مجموعة مثل B (المخرجات)، حيث تُسمى A مجال العلاقة، وأما المجموعة B فتتضمن عناصر المدى جميعها، وهناك أربع طرق لتمثيل العلاقة بين مجموعتين من الأعداد الحقيقية هي: 1 لفظيًّا : جملة تصف كيفية ارتباط عناصر المجال (3) بيانيا : تحديد نقاط في المستوى الإحداثي تمثل الأزواج المرتبة. بعناصر المدى. مثلا يرتبط كل عنصر من المجال بالعنصر الذي يزيد عليه قيمة بمقدار 2 من المدى. (2 عدديًا : جدول من القيم أو مخطط سهمي مجموعة من الأزواج المرتبة تربط عنصرًا من المجال (قيمة )x) بعنصر من المدى (قيمة y). أو (4) جبريًا: معادلة جبرية تربط بين الإحداثيين x,y لكل زوج من الأزواج المرتبة. مثلا: 2 + y = x {(0, 2), (1, 3), (2, 4), (3, 5)}: s إرشادات للدراسة المجال والمدى في هذا المفهوم الأساسي يمكن أن يستعمل الرمز D للتعبير عن المجال، والرمز أما الدالة فهي حالة خاصة من العلاقة. مفهوم أساسي الدالة التعبير اللفظي : الدالة f من مجموعة A إلى مجموعة B هي علاقة تربط كل عنصر x من المجموعة A مثال : R للتعبير عن المدى، أي أن: D = {1, 2, 3, 4} R = {6, 8, 9} بعنصر واحد فقط ل من المجموعة .B. العلاقة من المجموعة A إلى المجموعة B الممثّلة في المخطط المجاور تمثل دالة. حيث تمثل المجموعة A مجال الدالة. المجال = {4 ,3 ,2 ,1}. وتتضمن المجموعة B مدى الدالة. المجموعة B المجموعة A 6789 -23 4 المدى = 6,8,9 وزارة التعليم الدرس 1 - 1 الدوال M9try 2024-1446

رموز الفترات
استعمال رمز الفترة
تمييز الدالة
الدالة
2A- اكتب كلا من المجموعات الآتية باستعمال رمز الفترة:
غير محدودة
الرمزان
المجال والمدى
إرشادات للدراسة جدوليًا : إذا قطع الخط الرأسي التمثيل البياني في أكثر من نقطة، فإن إحدى قيم x ترتبط بأكثر من قيمة من قيم لا ، يوضح الجدول أدناه: x -2 -4 3 -1 3 4 ما 5 7 69 6 كما كما يمكن تعريف الدالة على أنها مجموعة من الأزواج المرتبة التي لا يتساوى فيها الإحداثي x لزوجين مختلفين، وهندسيا لا يمكن لنقطتين من نقاط الدالة أن تقعا على مستقيم رأسي واحد في المستوى الإحداثي . مفهوم أساسي اختبار الخط الرأسي التعبير اللفظي : تُمَثْلُ مجموعة من النقاط في المستوى الإحداثي دالة إذا لم يقطع أي خط رأسي تمثيلها البياني في أكثر من نقطة. النموذج : x مثال 3 تحديد العلاقات التي تمثل دوال في كل علاقة مما يأتي، حدد ما إذا كانت لا تمثل دالةً في x أم لا: a تمثل قيم x رقم الطالب، وقيم y درجته في اختبار الفيزياء. ترتبط كل قيمة لـ ا بقيمة واحدة لـ y ؛ إذ لا يمكن للطالب الحصول على درجتين مختلفتين في اختبار واحد؛ لذا فإن y تمثل دالةً في x إرشادات للدراسة دوال تتكرر فيها قيم ل : لا يمكن أن ترتبط أكثر من قيمة لـ لا بقيمة واحدة لـ x في الدالة، بينما يمكن أن ترتبط قيمة واحدة لـ y بأكثر من قيمة لـ x كما في المثال .3b (b x -8 -5 -5 -4 0 -3 548 3 -2 6 -3 ترتبط كل قيمة لـ x بقيمة واحدة لـ y ، وعليه فإن لا تمثل دالة في x . y² - 2x = 5 (d y (c 4 8x -4 -8 بما أنه يوجد خط رأسي مثل : 4 = x يقطع التمثيل البياني في أكثر من نقطة ، فإن لا لا تمثل دالة في x . كي تحدد ما إذا كانت لا تمثل دالةً في x ، حل المعادلة بالنسبة لـ y. المعادلة الأصلية أضف 2x لكلا الطرفين y2 - 2x = 5 y2 = 5 + 2x y = ± V5 + 2x خذ الجذر التربيعي لكلا الطرفين لا لا تمثل دالةً في x ؛ لأن كل قيمة من قيم x الأكبر من 2.5- ترتبط بقيمتين لـ y ، إحداها موجبة ، والأخرى سالبة. تحقق من فهمك (3) تمثل قيم x كمية الاستهلاك الشهري لأسرة من الكهرباء، أما قيم لا فتمثل المبلغ المستحق مقابل الاستهلاك. وزارة التعليم Ministry of Education 2024-1446 3y + 6x = 18 (3D YA 4 8x -8-4 -8 (3 (3B x y -6 -7 2 3 LO 5 8 5 9 9 22 الفصل 1 تحليل الدوال 10

اختبار الخط الرأسي
تحديد العلاقات التي تمثل دوال
3A- في كل علاقة فيما يأتي، حدد ما إذا كانت y تمثل دالة في x أم لا:
جدوليا
دوال تتكرر فيها قيم y
الربط مع تاريخ الرياضيات ليونارد أويلر (1783م - 1707م) عالم رياضي سويسري كتب أكثر من 800 بحث في الرياضيات، وهو أول من استعمل رمز الدالة (f(x . إرشادات للدراسة مجال الدالة : يمكنك كتابة مجال الدالة في المثال 5a بالطريقة المختصرة بالشكل D = R – {0, 7} إرشادات للدراسة تسمية الدوال : يمكنك التعبير عن الدالة ومتغيرها المستقل برموز أخرى فمثلا f(x) = V - 5 x- و 5 - t) = VE) يعبران عن الدالة نفسها. يُستعمل (f(x رمزًا للدالة ، ويُقرأ ( f الـ x ) ويعني قيمة الدالة عند x . وبما أن (f(x تمثل قيمة y التي ترتبط بقيمة x ، فإننا نكتب: (y = f(x . المعادلة y = -6x الدالة المرتبطة بالمعادلة f(x) = -6x يمثل المتغير x قيم المجال ويسمى متغيّرا مستقلا. ويمثل المتغير لا قيم المدى ويسمى متغيّرا تابعاً. مثال 4 إيجاد قيم الدالة إذا كان 24 - f(x) = x 2 + x ، فأوجد قيمة الدالة في كل مما يأتي: f(6) (a لإيجاد (6) f، عوّض 6 مكان x في الدالة 24 - f(x) = x2 + 8x . 24 - f(x) = x2 + 8x الدالة الأصلية - 24 - (6)8 + 2(6) = (6)f عوض 6 مكان x = 36 + 48 - 24 = = 60 f(-4x) (b بسط بسط f(x) = x2 + 8x - 24 f(-4x) = (-4x)² + 8(-4x) - 24 16x232x-24 f(5c+4) (c = الدالة الأصلية عوض 4x- مكان x بسط f(x) = x2 + 8x - 24 f(5c+ 4) = (5c+ 4)² + 8(5c+4) — 24 - = 25c2 + 400 + 16 + 400 + 32 - 24 2x + 3 تحقق من فهمك إذا كانت - 2x + 1 f(12) (4A 43 = 25c2 + 80c + 24 = الدالة الأصلية عوض 4 + 5 مكان x فك الأقواس 4 + 5c) و (4 + 85 بسط (f(x، فأوجد قيمة الدالة في كل مما يأتي: f(6x) (4B f(-3a +8) (4C إذا لم يذكر مجال الدالة فإنه يكون مجموعة الأعداد الحقيقية، مع استثناء القيم التي تجعل مقام الكسر صفرًا أو تجعل ما تحت الجذر عددًا سالبًا إذا كان دليل الجذر زوجيًّا. مثال 5 حدد مجال كل من الدوال الآتية: تحديد مجال الدالة جبريًّا f(x) = 2+x x2 - 7x (a 2 + x x2 - 7x تكون العبارة غیر معرّفة إذا كان المقام صفرًا، وبحل المعادلة 0 = x 2 - 7x ، فإن القيم المستثناة 0 = x و 7 = x ، وعليه يكون مجال الدالة هو مجموعة الأعداد الحقيقية عدا 0 = من المجال هي - x = = R} s₁₁x = 7, g(t)=√√t-5 (b .D = (−∞, 0) U(0, 7) U(7, ∞) † D= {x | x 0, x 7, x بما أن الجذر التربيعي للعدد السالب غير معرف، فيجب أن تكون 0 5 - t ؛ أي أن مجال الدالة 8 هو مجموعة الأعداد الحقيقية الأكبر من أو تساوي 5 أي أن , D = x | x أو ( ,5] = D. وزارة التعليم الدرس 1 - 1 الدوال Misty of E 2024-1446

ايجاد قيم الدالة
تحديد مجال الدالة جبرياً
يستعمل f(x) رمزا للدالة
4A- أوجد قيمة الدالة في كل مما يأتي:
ليونارد أويلر (1707-1783)م
مجال الدالة
تسمية الدوال
1 h(x) = (c x2 - 9 تكون هذه الدالة معرّفة إذا كان المقام معرفًا، وقيمته لا تساوي صفرًا، وهذا يعني أنها معرفة عندما يكون 0 < 9 - x2 ، وعليه فإن 9 < x2 وهذا يعني أن 3 < | x | ؛ لأن | Vx2 = | x ، ويكون مجال (h (x .D = (— ∞, −3) U (3, ∞) ‚† D= {x|x < −3 g¡ x > 3, x ЄR} s 8x g(x) = (5C h(a) = Va2 – 4 (5B f(x) : = V2x + 6 تحقق من فهمك 5x-2 (5A x2 + 7x + 12 تُعرف بعض الدوال بقاعدتين أو أكثر وعلى فترات مختلفة ، وتُسمّى مثل هذه الدوال الدوال المتعددة التعريف. مثال 6 من واقع الحياة إيجاد قيم الدالة المتعددة التعريف طول : إذا كانت العلاقة بين أكبر معدل لطول الطفل ( بالبوصة، وأكبر طول لوالديه x بالبوصة معطاة بالدالة: h(x) = { 1.6x-41.6, 3x-132 2x-66 ' 63 < x < 66 66 < x < 68 x > 68 فأوجد أكبر معدل لطول الطفل في كل من الحالتين الآتيتين: a أكبر طول لوالديه 67 بوصة. بما أن 67 واقعة بين 66 و 68 ، فإننا نستعمل القاعدة 132 - x) = 3x) لإيجاد (67). h(x)=3x132 h(67) = 3(67) - 132 =201 - 132 = 69 تعريف الدالة في الفترة 68 = x ≥ 66 عوض 67 مكان x بسط بناءً على هذه الإجابة فإن الطفل الذي يبلغ أكبر طول لوالديه 67 بوصة ، يكون أكبر معدل ممكن لطوله 69 بوصة. b أكبر طول لوالديه 72 بوصة. بما أن 72 أكبر من 68 ، فإننا نستعمل القاعدة 66 - h(x) = 2x لايجاد (72)h . h(x)=2x-66 h(72) = 2(72) - 66 = 144 - 66 = 78 تعريف الدالة في الفترة 68 < x عوض 72 مكان x بسط إرشادات للدراسة سرعة السيارة : تقاس سرعة السيارة عادة بالميل أو بالكيلومتر لكل بناءً على هذه الإجابة، فإن الطفل الذي يبلغ أكبر طول لوالديه 72 بوصة، يكون أكبر معدل ممكن لطوله 78 بوصة. تحقق من فهمك 6) سرعة: إذا كانت سرعة مركبة )) بالميل لكل ساعة تُعطى بالدالة المتعددة التعريف الآتية، حيث الزمن t بالثواني: ساعة، ويمكن أن تتغير كل ثانية ما لم يستعمل مثبت السرعة. فأوجد كلا مما يأتي: v(5) (6A 4t 0 ≤ t ≤ 15 v(t) = 60 15 < t < 240 ' -6t + 1500 240 ≤ t < 250 v(245) (6C v(15) (6B وزارة التعليم Ministry of Education 2024-1446 الفصل 1 تحليل الدوال 12

تكون هذه الدالة معرفة إذا كان المقام معرفا، وقيمته لا تساوي صفرا
ايجاد قيم الدالة المتعددة التعريف
5A- حدد مجال كل من الدوال الآتية:
6A- أوجد كلا مما يأتي:
سرعة السيارة
g(x) = 3x3 x2 + x 4 ― g(-2) (a g(5x) (b g(84b) (c (22 g(m) = 3 + Vm2 - 4 (23) g(-2) (a g(3m) (b g(4m - 2) (c t(x) = 5√√√6x² (24 t(-4) (a t(2x) (b t(7+n) (c (25) مبيعات : قدرت مبيعات شركة المبيعات بملايين السنة للسيارات خلال خمس سنوات بالدالة: 78 + f(t) = 24t2 – 93t، حيث الزمن بالسنوات، وكانت المبيعات الفعلية موضحة في الجدول المجاور. ( مثال 4 ) a) أوجد (1)f. الريالات 1 1 3 2 14 3 74 4 219 5 ہے b) أوجد (5)f. تدرب وحل المسائل اكتب كل مجموعة مما يأتى باستعمال الصفة المميزة للمجموعة، وباستعمال رمز الفترة إن أمكن المثالان (12) x<-13 (2 {-3, -2, -1, ...} (4 6) 19 > x أو 21 < x x > 50 (1 x ≤ −4 (3 -31 < x = 64 (5) (7) 61 = x أو 67 = x (8) 45 = x أو 86 < x (9) المضاعفات الموجبة للعدد 5 10 32 < x في كل علاقة مما يأتي، حدد ما إذا كانت لا تمثل دالة في x أم لا: ( مثال 3 ) 11) المتغير المستقل x يمثل رقم الحساب في البنك، والمتغير لا يمثل الرصيد في الحساب x 0.01 423 449 0.04 0.04 0.07 0.08 0.09 451 466 (12 478 482 x2 · = y + 2 (14 = y (13 x A = - = y - 6 (16 y V48y = x (15 (18 y (17 48 0 x أوجد قيم كل دالة من الدوال الآتية: (مثال 4) هل تعتقد أن القاعدة (f (t أكثر دقة في السنة الأولى، أم في السنة الأخيرة؟ برّر إجابتك. حدد مجال كل دالة مما يأتي: ( مثال 5 ) g(x) = x + 1 x2 - 3x - 40 (27 (x) = V6 - x2 (29) f(x) = 28 4 + x + 1 f(x) = 8x + 12 (26 x2 + 5x + 4 (a) = V1 + a2 (28 = 5a (31 f(a) = (30 V4a - 1 12 11 1 19 2 3 8 7 6 (32) فيزياء: يعطى زمن الدورة T لبندول ساعة l 9.8 27 = T، حيث طول بالصيغة هو البندول، فهل تمثل T دالة في ؟ إذا كانت كذلك فحدّد مجالها، وإذا لم تكن دالة فبين السبب. (مثال 5 ) الطول . زمن الدورة T وزارة التعليم الدرس 1 - 1 الدوال M130fE 2024-1446 g(x) = 2x2 + 18x - 14 (19 g(9) (a g(3x) (b g(15m) (c h(y) = -3y3 - 6y + 9 (20 f(t) = = h(4) (a h(-2y) (b h(5b+3) (c 4t + 11 342 + 5 + 1 f(-6) (a f(4t) (b f(32a) (c (21

اكتب كل مجموعة مماياتي باستعمال الصفة المميزة للمجموعة، وباستعمال رمز الفترة إن أمكن:
في كل علاقة مما ياتي حدد ما اذا كانت y تمثل دالة في x أم لا:
اوجد قيم كل دالة من الدوال الاتية:
تابع اوجد قيم كل دالة من الدوال الاتية
أوجد f(1) .
26- حدد مجال كل دالة فيما ياتي:
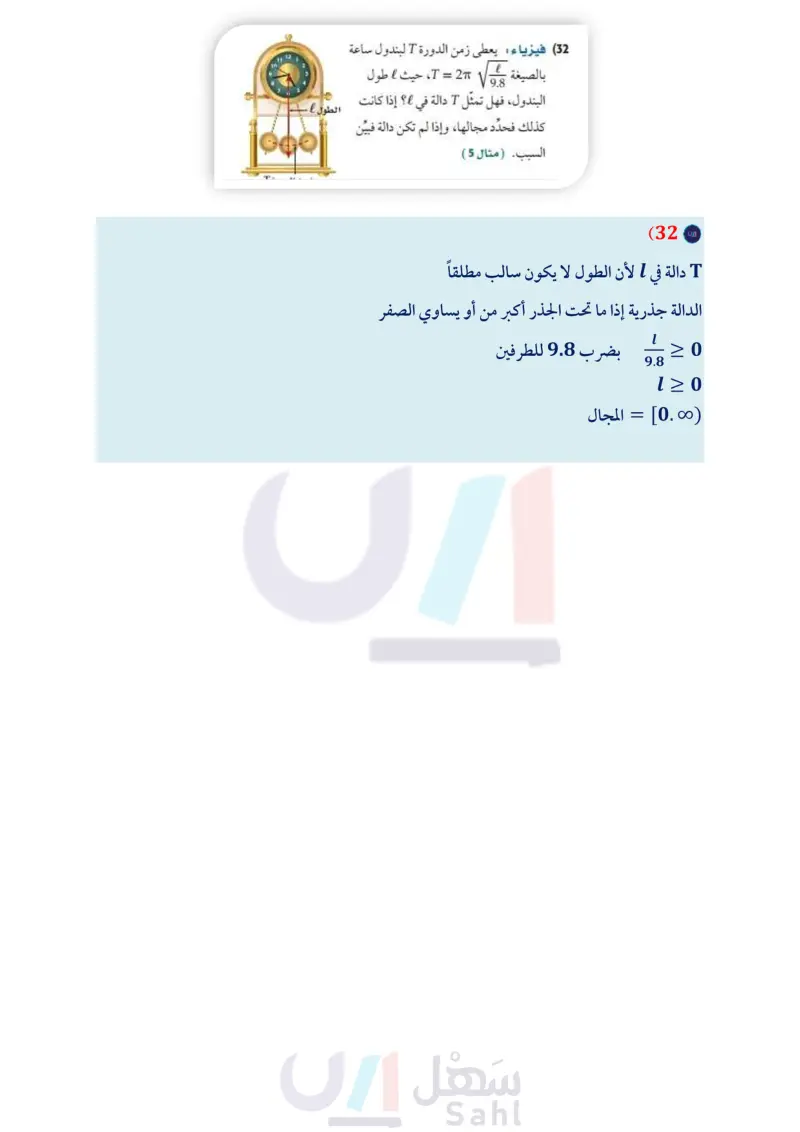
هل تمثل T داله في t ؟ إذا كانت كذلك فحدد مجالها، وإذا لم تكن دالة فبين السبب.
(39) هندسة : يمثل الشكل أدناه دائرة مساحتها A ومحيطها C. A C أوجد (5) وَ (12) لكلِّ من الدالتين الآتيتين: (مثال 6 ) -4x + 3 x < 3 f(x) = { x3 3x2 + 1 3≤ x ≤8 (33 ' x> 8 ' (34 -15 f(x) = { Vx + 6 x < -5 -5 < x < 10 2 +8 / x > 10 اكتب المساحة كدالة في المحيط. أوجد (0.5) (4) مقربًا إلى أقرب جزء من مئة. ما تأثير زيادة المحيط في المساحة ؟ (35 عمل تمثل الدالة (T (x أدناه الربح بالريال) الذي تكسبه شركة 40 حسابات تتناقص قيمة أجهزة الحاسوب بعد شرائها مع مرور الزمن. وتُستعمل الدوال الخطية لتمثيل هذا التناقص. فإذا كانت توزيع لأجهزة هاتف: t) = 1800 - 30 t) تمثل قيمة حاسوب بالريال، بعد t شهر من شراءه. فحدد مجال هذه الدالة. , (a), f (a + b) ، حيث 0 لكل مما يأتي: f(x) = √√x (42 f(x) = x2 - 6x + 8 (44) f(x) = x3 + 9 (46 f(x) = x3 (48 f(a + h) − f(a) - أوجد . h f(x) = −5 (41 f(x) 1 = (43 X + 4 f(x) = −14x+6 (45 2.1x 0 < x < 7000 ' T(x) = { 500 + 2.4 7000 < x < 20000 800 + 3x 20000 < x < 80000 حيث x تمثل عدد الأجهزة الموزّعة، فأوجد: T(7000), T(10000), T(50000) معتمدًا على اختبار الخط الرأسي ، حدد ما إذا كان كل من التمثيلين الآتيين يمثل دالة أم لا، وبرّر إجابتك. f(x) = 5x2 (47 00 4 (49) صناعة : في أحد المعامل الوطنية يتم صنع أحد المعامل الوطنية يتم صنع أغلفة بريدية متفاوتة الأبعاد، بحيث تكون نسبة طول الغلاف إلى عرضه من 1.3 إلى 2.5، فإذا كانت أصغر قيمة لطول الأغلفة المنتجة 5in ، وأكبر قيمة in 11 ، فأجب عما يأتي: -40 -8 (37 y 4 8x a y 18 (36 مسافة (38) رياضة : تتكون مسابقة رياضية من ثلاث مراحل: سباحة مسافة 0.4mi ، وقيادة دراجة هوائية مسافة 5mi ، وجري 2.6mi . فإذا كان معدل سر سرعة عزام في كل مرحلة من المراحل الثلاث كما في الجدول أدناه: المرحلة السباحة معدل السرعة قيادة الدراجة الجري 4mi/h 20 mi/h 6 mi/h اكتب دالة متعددة التعريف تمثّل المسافة D التي قطعها عزام بدلالة الزمن t. ) حدد مجال الدالة. الطول . العرض a اكتب مساحة الغلاف A كدالة في طوله ، إذا كانت نسبة طول الغلاف إلى عرضه 1.8 ، ثم اكتب مجال الدالة. اكتب مساحة الغلاف A كدالة في عرضه ، إذا كانت نسبة طول الغلاف إلى عرضه 2.1 ، ثم اكتب مجال الدالة. أوجد مساحة الغلاف عند أكبر طول ممكن له ، وأكبر نسبة بين طوله وعرضه. في كل من العلاقتين الآتيتين، حدد ما إذا كانت لا تمثل دالة في x أم لا. برّر إجابتك. وزارة التعليم Ministry of Education 2024-1446 x = y3 (51 x = |y| (50 الفصل 1 تحليل الدوال 14

أوجد f(12) و f(-5) لكل من الدالتين الأتيتين:
أوجد : T(7000), T(1000), T(50000) .
حدد ما اذا كان كل من التمثيلين الاتيين يمثل دالة أم لا، وبرر إجابتك.
اكتب دالة متعددة التعريف تمثل المسافة D التي قطعها عزام بدلالة الزمن t .
اكتب المساحة كدالة في المحيط.
حدد مجال هذة الدالة.
41- أوجد f(a) لكل مما يأتي :
اكتب مساحة الغلاف كدالة في طوله l إذا كانت نسبة طول الغلاف إلى عرضه 1.8 ثم اكتب مجال الدالة.
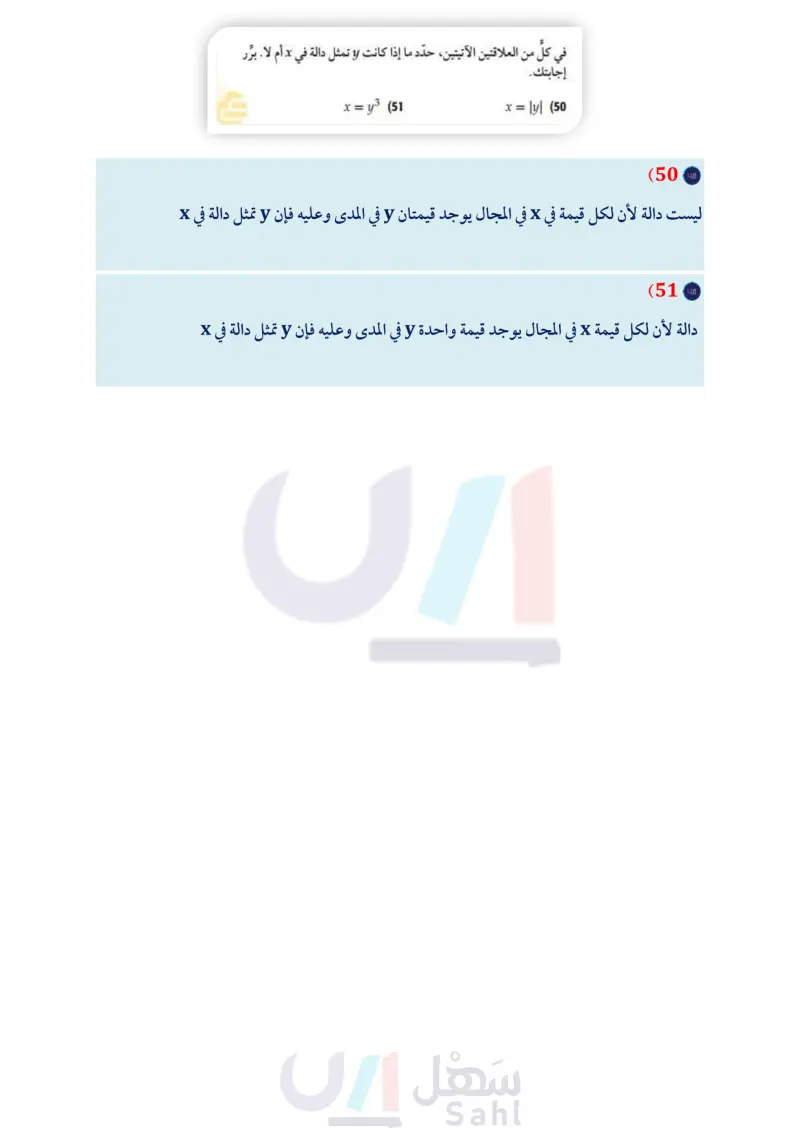
في كل من العلاقتين الاتيتين حدد ما إذا كانت y دالة في x أم لا، برر إجابتك.
r²-7r - 30 r2 – 5r – 24 ☐ + 1 22 - 1 4 1 (52) تمثيلات متعددة : تمثيلات متعددة : سوف تستقصي في هذه المسألة مدى الدالة f(x) = xn ، حيث neN. a بيانيا : استعمل الحاسبة البيانية لتمثل الدالة "f(x) = x بيانيا لقيم n الصحيحة من 1 إلى 6. مراجعة تراكمية بسط كل عبارة مما يأتي: (مهارة سابقة) (65 2r - 4 (64 r 2 107y 17 (67 اد 4y Зу + (66 4 4x 3x -10 1 16 6x2 - 11x + 4 12x2 + 11x+2 . (68 6x 2 + x - 2 8x2 + 14x + 3 -10 f1(x)=x2 1.1▸ 10 (b جدوليًا : تنبأ بمدى كل دالة من الدوال التي مثلتها في الفرع a، : واعرضه في جدول يتضمن قيم ، ، والمدى المرتبط بكل منها. حل كلًا من المعادلتين الآتيتين: (مهارة سابقة) لفظيًّا : خمّن مدى الدالة (f(x عندما يكون n زوجيًا. d) لفظيًا : خمّن مدى الدالة (f(x عندما يكون n فرديًا. مسائل مهارات التفكير العليا (53) اكتشف الخطأ : أراد كلّ من عبد الله وسلمان تحديد مجال الدالة 2 = x2 ― 4 = (f(x . فقال عبد الله : إن المجال هو (2,00) U (2) . في حين قال سلمان : أن المجال هو 1 X 2 -플=클 3 8 (70 2 $ = 1 + 2 x-2 (69 حل كلا من المتباينتين الآتيتين: (مهارة سابقة) +2≥0 (72 x + 1 x - 3 -1≤2 (71 {x | x - 2, x + 2, x e R . فأيهما كانت إجابته صحيحة ؟ برّر تدريب على اختبار إجابتك. 68 (54) اكتب مجال الدالة 1 = (x + 3)(x + 1)(x — 5) - (73) أي العبارات الآتية صحيحة دائمًا : (f(x باستعمال كل من رمز الفترة والصفة المميزة للمجموعة . أي الطريقتين تفضل؟ الدالة لا تمثل علاقة. ولماذا ؟ كل دالة تمثل علاقة. (55) تحد : إذا كانت (G(x دالة فيها 3 = (3) = (2)G(1) = 1, G كل علاقة تمثل دالة. = G(x 2) G(x 1) +1 ― G(x) (1) + )x) لكل 3 < x ، فأوجد(6)G. العلاقة لا تكون دالة. وزارة التعليم الدرس 1 - 1 الدوال Mi150E 2024-1446 تبرير: أيُّ الجمل الآتية تصف الدالة المعرفة من المجموعة X إلى المجموعة Y بشكل صحيح، وأيها خاطئة، وإذا كانت خاطئة، فأعد كتابتها (74) أي مما يأتي يمثل مجال الدالة: لتصبح صحيحة. (56) يرتبط كل عنصر من Y بعنصر واحد من X. (57) لا يرتبط عنصران أو أكثر من X بالعنصر نفسه من Y . 58 لا يرتبط عنصران أو أكثر من Y بالعنصر نفسه من X . اكتب وضح كيف يمكنك تحديد الدالة من خلال: (59) جملة لفظية تبيّن العلاقة بين عناصر المجال وعناصر المدى. (60) مجموعة أزواج مرتبة. 61) جدول قيم. (62) تمثيل بياني (63) معادلة. h(x) = √2x-3 x-5 x5 A 3 B X> x #5 C x * D

تنبأ بمدى كل دالة من الدوال التي مثلتها في الفرع a واعرضه في جدول يتضمن قيم n والمدى المرتبط بكل منها.
64- بسط كل عبارة مما يأتي:
69- حل كلا من المعادلتين الاتيتين:
71- حل كلا من المتباينتين الاتيتين:
أي العبارات الاتية صحيحة دائما:
أي مما ياتي يمثل مجال الدالة:
ايهما كانت اجابتة صحيحة ؟ برر إجابتك.
أكتب مجال الدالة باستعمال كل من رمز الفترة والصفة المميزة للمجموعة. أي الطريقتين تفضل ؟ ولماذا ؟
اوجد G(6) .
أي الجمل الآتية تصف الدالة المعرفة من مجموعة x إلى المجموعة Y بشكل صحيح، وأيهما خاطئة. وإذا كانت خاطئة فأعد كتابتها لتصبح صحيحة.
وضح كيف يمكنك تحديد الدالة من خلال :