قطع مستقيمة خاصة في الدائرة - رياضيات 1-3 - أول ثانوي

وزارة التعليم Ministry of Education 2024-1446 www.icm.edu.sa قطع مستقيمة خاصة في الدائرة Special Segments in a Circle 8-7 اليسا سبق درست إيجاد قياس الأقطار التي تتقاطع لماذا؟ قطعت كعكة دائرية كبيرة طوليا لتكفي أكبر عدد ممكن من المدعوين إلى حفلة، ولم يبق منها إلا قطعة صغيرة. يمكنك داخل متوازي الأضلاع. إيجاد قطر الكعكة الأصلية باستعمال الخصائص الهندسية (مهارة سابقة ) وانان - أجد قياسات الأوتار المتقاطعة داخل الدائرة. - أجد قياسات القطع للدائرة. الأوتار المتقاطعة داخل الدائرة: عندما يتقاطع وتران داخل دائرة، ينقسم كل منهما جزأين، ففي الشكل المجاور ، انقسم الوتر AC إلى AB و BC ، وكذلك انقسم الوتر ED إلى EB و BD. D A E C المستقيمة المتقاطعة تصف النظرية الآتية العلاقة بين القطع المستقيمة الأربع التي تكونت من تقاطع وترين داخل دائرة. خارج الدائرة. نظرية 8.15 نظرية قطع الوتر التعبير اللفظي: إذا تقاطع وتران في دائرة، فإن حاصل ضرب طولي جزأي الوتر الأول يساوي حاصل ضرب طولي جزأي الوتر الثاني. D أضف إلى مطويتك A E B C AB· BC = DB.BE مثال: ستبرهن النظرية 8.15 في السؤال 15 مثال 1 استعمال تقاطع الوترين أوجد قيمة : في كل من الشكلين الآتيين: النظرية 8.15 بالتعويض بالضرب بقسمة كلا الطرفين على 10 النظرية 8.15 بالتعويض بالضرب بطرح " من كلا الطرفين بطرح 9x من كلا الطرفين AB.BC = EB.BD D (a 5.12 = x 10 A 5 10 B 60 = 10x 6 = x x E 12 C JK. KL = (x+10) x PK. KM (x+1)(x+8) P (b x+1 x2 + 10x = x 2 + x + 8 L x + 10 K 10x = 9x + 8 x+8 x= 8 أوجد قيمة x في كل من الشكلين الآتيين : W X x+2 (18) 21 + 6 1x + 12 Y 6 P R 15 4 x T S M تحقق من فهمك (1A الفصل 8 الدائرة 164

مثال 2 من واقع الحياة إيجاد قياس قطع مستقيمة في الدائرة علوم: شكل قوس المطر الحقيقي دائرة كاملة، ولا يظهر لنا منها إلا القوس الذي يظهر فوق أفق الكرة الأرضية. ما نصف قطر الدائرة التي تحوي قوس المطر الظاهر في الشكل أدناه؟ 10.7 mi B 5.mi الربط مع الحياة كلما كانت الشمس قريبة من الأفق، زاد الجزء الذي تراه من قوس المطر. وعند غروب الشمس يمكنك رؤية قوس المطر على شكل نصف دائرة بحيث تصنع أعلى نقطة في هذا القوس زاوية مقدارها 42 درجة فوق الأفق. افهم المعطيات قوس المطر الظاهر جزء من دائرة AC وتر في الدائرة DB عمود منصف للوتر AC المطلوب إيجاد طول نصف قطر الدائرة التي تحوي قوس المطر الظاهر. خطط ارسم نموذجًا للمسألة بما أن DE تُنصف الوتر AC ، فإن DE قطر في الدائرة. استعمل ناتج ضرب أطوال الأوتار المتقاطعة لإيجاد طول ١٢ قطر الدائرة. حل AB.BC = DB.BE 2.5 . 2.5 = 0.7. BE 6.25 = 0.7BE النظرية 8.15 بالتعويض بالضرب D B0.7 2.5 2.5 E A إرشادات لحل المسألة ارسم شكلا : عند حل المسائل اللفظية المتعلقة بالدوائر يُفضّل أن ترسم شكلا وتضع عليه قياسات كل عناصر الدائرة المعطاة وأن تسمي القياس المجهول برمز متغير لمساعدتك على اختيار خطة الحل المناسبة. 8.9 = BE DE = DB + BE ≈ 0.7 + 8.9 = 9.6 بقسمة كلا الطرفين على 0.7 مسلمة جمع القطع المستقيمة بالتعويض بالجمع بما أن قطر الدائرة يساوي 9.6mi تقريباً، فإن نصف قطرها يساوي 4.8 × 2 : 9.6 تحقق استعمل عكس نظرية فيثاغورس؛ للتحقق من أن المثلث المتكوّن من نصف القطر وجزء من الوتر وجزء من القطر في الدائرة قائم الزاوية. DB + BF = DF 0.7 + BF = 4.8 BF = 4.1 جمع القطع المستقيمة مسلمة. بالتعويض بطرح 0.7 من الطرفين D A B0.7 2.5 2.5 C 4.8 Fi 4.8 E BF2 + BC2 = Ce 4.12 +2.524.8² 23.06 23.04✓ اتحقق من فهمك نظرية فيثاغورس بالتعويض بالتبسيط (2) مصلى قبة الصخرة هو أحد أهم معالم المسجد الأقصى المبارك في مدينة القدس، وتعتبر قبته من أهم وأبرز المعالم المعمارية الإسلامية، فهي عبارة عن قبة كروية قطر الدائرة التي تحتوي على القوس المار بالقمة هي 20m ، ويبلغ ارتفاع أعلى نقطة فيها عن الجزء الأسطواني الذي يحملها 15m، أوجد المسافة بين طرفي القبة ؟ الدرس 7-8 قطع مستقيمة خاصة في الدائرة ال165م Ministry of Education 2024-1446

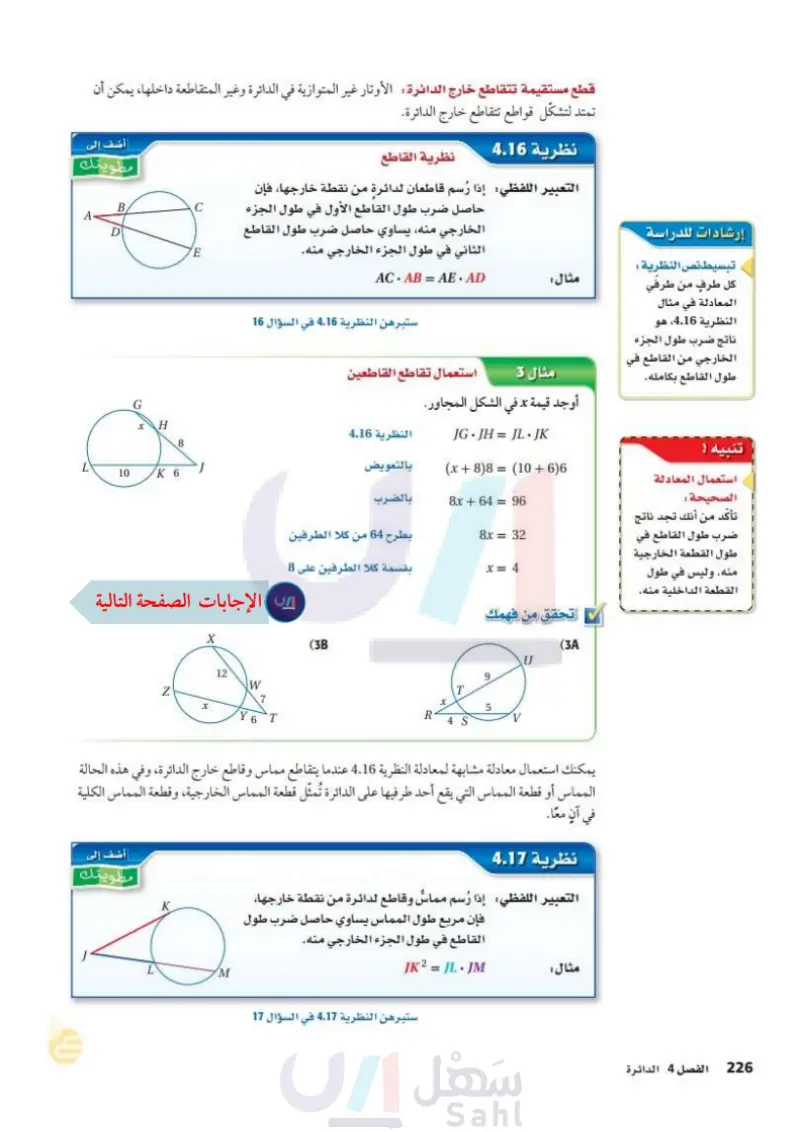
قطع مستقيمة تتقاطع خارج الدائرة الأوتار غير المتوازية في الدائرة وغير المتقاطعة داخلها، يمكن أن تمتد لتشكل قواطع تتقاطع خارج الدائرة. نظرية 8.16 نظرية القاطع التعبير اللفظي: إذا رُسم قاطعان لدائرة من نقطة خارجها، فإن مطويتك B/ C A G x H 8 10 K 6 X إرشادات للدراسة تبسيط نص النظرية : كل طرف من طرفي المعادلة في مثال النظرية 8.16، هو ناتج ضرب طول الجزء الخارجي من القاطع في طول القاطع بكامله. مثال: مثال 3 حاصل ضرب طول القاطع الأول في طول الجزء الخارجي منه يساوي حاصل ضرب طول القاطع الثاني في طول الجزء الخارجي منه ACAB = AE. AD ستبرهن النظرية 8.16 في السؤال 16 استعمال تقاطع القاطعين أوجد قيمة x في الشكل المجاور. 12 W 7 x 6 T النظرية 8.16 بالتعويض بالضرب بطرح 64 من كلا الطرفين بقسمة كلا الطرفين على 8 (38) R JG. JH = JL.JK = (x+8)8 (106)6 8x + 64 = 96 8x = 32 x= 4 تحقق من فهمك (3) U 9 T 5 4 S V يمكنك استعمال معادلة مشابهة لمعادلة النظرية 8.16 عندما يتقاطع مماس وقاطع خارج الدائرة، وفي هذه الحالة المماس أو قطعة المماس التي يقع أحد طرفيها على الدائرة تُمثل قطعة المماس الخارجية، وقطعة المماس الكلية أضف إلى مطويتك وزارة التعليم Ministry of Education 2024-1446 K M في آن معا. نظرية 8.17 التعبير اللفظي إذا رسم مماس وقاطع لدائرة من نقطة خارجها، فإن مربع طول المماس يساوي حاصل ضرب طول القاطع في طول الجزء الخارجي منه. JK²=JL. JM ستبرهن النظرية 8.17 في السؤال 17 مثال: تنبيه ! استعمال المعادلة الصحيحة : تأكد من أنك تجد ناتج ضرب طول القاطع في طول القطعة الخارجية منه. وليس في طول القطعة الداخلية منه. الفصل 8 الدائرة 166

A P 8 S 7 مثال 4 استعمال المماس والقاطع إذا كانت في مماشا للدائرة كما في الشكل المجاور، فأوجد قيمة لا مقربا إجابتك إلى أقرب علي Ci D 10 B النظرية 8.17 بالتعويض بالضرب PQ²=QR.QS 8² = x(x+7) 64 = x2 + 7x 0 = x2 + 7x - 64 بطرح 64 من كلا الطرفين استعمل القانون العام لحل المعادلة التربيعية؛ لأن المقدار غير قابل للتحليل. القانون العام a = 1, b = 7, c = -64 بالتبسيط x= -b±√b²-4ac 20 -7±√√72-4(1)(-64) 2(1) -7± √305 2 5.2 أو 12.2-= باستعمال الحاسبة وبما أنه لا يمكن أن تكون الأطوال سالبة، فإن قيمة x تساوي 5.2 تقريباً. اتحقق من فهمك 4) AB مماس للدائرة في الشكل المجاور، أوجد قيمة x مقربًا إجابتك إلى أقرب عُشر. تأكد الأمثلة 1.3.4 أوجد قيمة ، في كل من الأشكال الآنية، مفترضا أن القطع المستقيمة التي تبدو مماسات للدائرة، هي مماسات فعلا. Z (2 W x+3 Y x+9 P X+4 پیار X x D A 5 7.5 C 4.5 E 6 cm 10 cm_D $ 10 cm (4 G S R. x 4 4T 8 U H 4 J K 6 المثال 2 (5) آثار يبين الشكل المجاور صورة جزء مكسور من إناء فخاري دائري وجد في موقع أثري. إذا كانت 25 جزءا من قطر الدائرة، فما محيط الإناء الفخاري الأصلي؟ قرب إجابتك إلى أقرب جزء من مئة. الدرس 7-8 قطع مستقيمة خاصة في الدائرة الت167م Ministry of Education 2024-1446

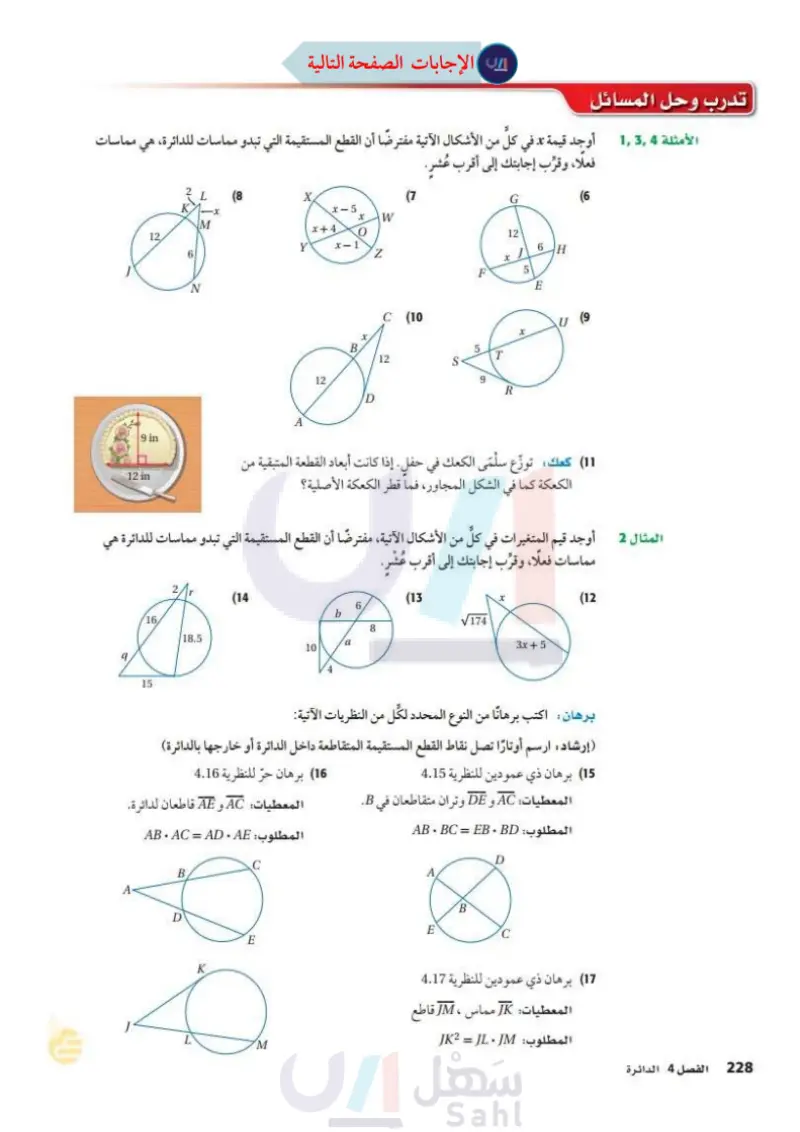
وزارة التعليم Ministry of Education 2024-1446 تدرب وحل المسائل الأمثلة 134 أوجد قيمة تد في كل من الأشكال الآتية مفترضًا أن القطع المستقيمة التي تبدو مماسات للدائرة، هي مماسات فعلا، وقرب إجابتك إلى الغرب عشر. 9 in 12, 6 2 L X (7 x-5 G M x W x+4 0 12 Y X-1 Z 6 H N F 5 E A C (10 U B 5 12 S T 12 D 9 R (6) (11) كعك: توزّع سلمى الكعك في حفل. إذا كانت أبعاد القطعة المتبقية من الكعكة كما في الشكل المجاور، فما قطر الكعكة الأصلية؟ 12 in المثال 2 أوجد قيم المتغيرات في كلّ من الأشكال الآتية، مفترضًا أن القطع المستقيمة التي تبدو مماسات للدائرة هي مماسات فعلا، وقرب إجابتك إلى أقرب عُشر. 16, 18.5 9 15 (14 6. (13 x b 8 174 10 a 3x+5 (12) برهان اكتب برهانا من النوع المحدد لكل من النظريات الآتية: (إرشاد ارسم أوتارا تصل نقاط القطع المستقيمة المتقاطعة داخل الدائرة أو خارجها بالدائرة) (15) برهان ذي عمودين للنظرية 8.15 المعطيات: AC و DE وتران متقاطعان في B. المطلوب : AB.BC = EB-BD (16) برهان حر للنظرية 8.16 المعطيات: AC و AE قاطعان لدائرة. المطلوب : AB. AC = AD.AE A D B E C E B DA K (17) برهان ذي عمودين للنظرية 8.17 المعطيات: JK مماس ، JM قاطع المطلوب : JK2 = JL . JM الفصل 8 الدائرة 168

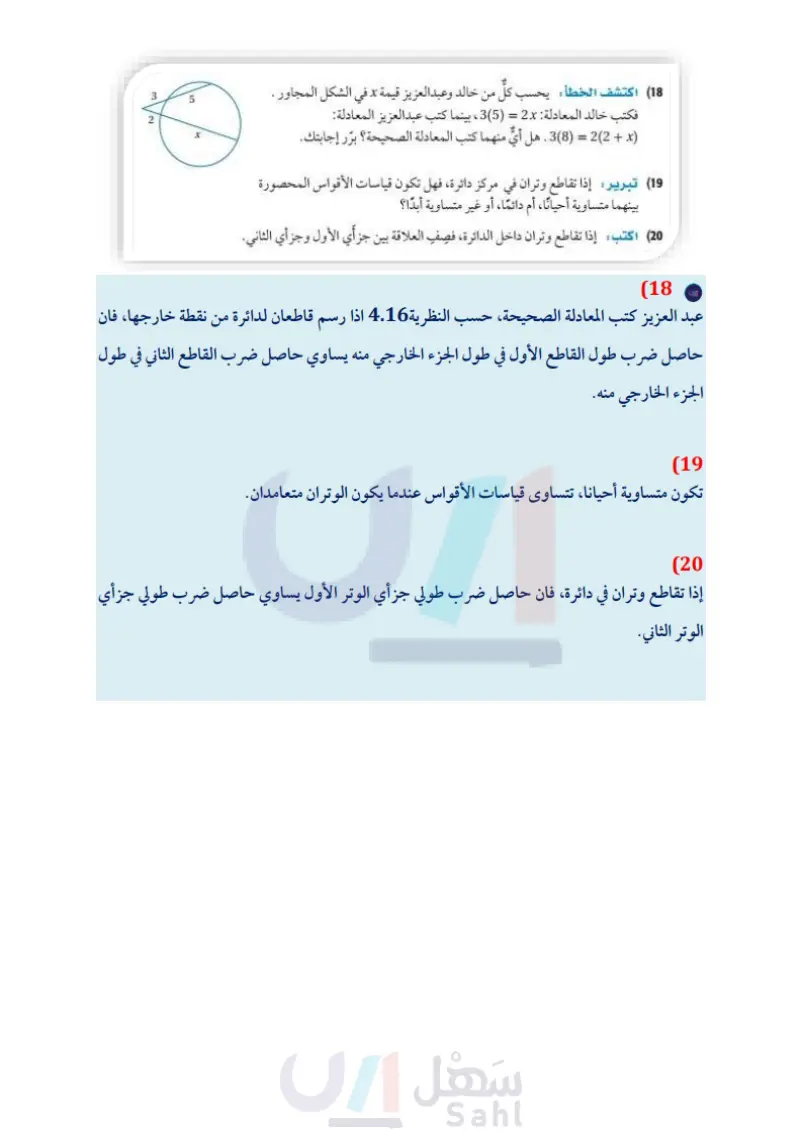
A 5 مسائل مهارات التفكير العليا 18 اكتشف الخطأ: يحسب كل من خالد وعبد العزيز قيمة x في الشكل المجاور . فكتب خالد المعادلة : 2x = (5)3 ، بينما كتب عبدالعزيز المعادلة: x + 22 = (38) . هل أي منهما كتب المعادلة الصحيحة؟ برر إجابتك. 19) تبرير: إذا تقاطع وتران في مركز دائرة، فهل تكون قياسات الأقواس المحصورة بينهما متساوية أحيانا، أم دانشاء أو غير متساوية أبدا؟ 20 اكتب إذا تقاطع وتران داخل الدائرة، فصف العلاقة بين جزاي الأول وجزأي الثاني. تدريب على اختبار (21) TV مماس للدائرة، و R, S نقطتان عليها ، ما قيمة x مقربةً إلى (22) إجابة مطولة : MBA,BC مماسان للدائرة في الشكل أدناه، B mZABC= 70° A a) اكتب معادلتين تربطان بين x و y . أوجد قيمة كل من بدو تو. 5.7 C 4.8 D x R T x+3 9 V أقرب عشر؟ 7.6 A 6.4 B مراجعة تراكمية (23) نسيج بعد أن تُغزل خيوط الصوف، يتم صبغها، ثم تُمرّر على مجموعة من البكرات لكي تجف، والشكل المجاور يُظهر إحدى مجموعات البكرات، لاحظ أن خيط الصوف يبدو كأنه يتقاطع بعضه مع بعض عند النقطة C، ولكنه في الواقع غير ذلك. أوجد mBH مستعملاً معلومات الشكل (الدرس 6-8) 116' F B 38 D H E هندسة إحداثية مثل بيانيا الشكل وصورته الناتجة عن الإزاحة المعطاة في كل مما يأتي : ( الدرس 2-8 ) 24 KLM الذي رؤوسه 2010 (5)؛ إزاحة مقدارها 3 وحدات إلى اليسار و 4 وحدات إلى أسفل. (25) الشكل الرباعي PQRS الذي رؤوسه: 4-2-2 - )R ,(1,4 - )2 ,(1,4)؛ إزاحة مقدارها 5 وحدات إلى اليسار و 3 وحدات m = 5, (0, -6) (28 m=- 12 b: 1 (31 الدرس 7-8 قطع مستقيمة خاصة في الدائرة ال169م Ministry of Education 2024-1446 إلى أعلى. استعد للدرس اللاحق اكتب بصيغة الميل والمقطع معادلة المستقيم الذي عليم ميله ومقطع لاله في كل مما يأتي: m=2, (0,8) (27 m = -1, b: -3 (30 (26) 3 : 2 المقطع 1 = 4 29) 3 : m، المقطع y = 3 m: