الرياضيات 1 الفصل2: التوازي والتعامد 2-4 ميل المستقيم

ميل المستقيم - الرياضيات 1 - أول ثانوي

القسم الأول

الفصل1: التبرير والبرهان

التهيئة للفصل 1

1-1 التبرير الاستقرائي والتخمين

1-2 المنطق

1-3 العبارات الشرطية

توسع1-3 العبارات الشرطية الثنائية

1-4 التبرير الاستنتاجي

1-5 المسلمات والبراهين الحرة

1-6 البرهان الجبري

1-7 إثبات علاقات بين القطع المستقيمة

1-8 إثبات علاقات بين الزوايا

الفصل2: التوازي والتعامد

التهيئة للفصل 2

2-1 المستقيمان والقاطع

استكشاف 2-2 الزوايا والمستقيمات المتوازية

2-2 الزوايا والمستقيمات المتوازية

2-3 إثبات توازي مستقيمين

2-4 ميل المستقيم

2-5 صيغ معادلة المستقيم

توسع 5-2 معادلة العمود المنصف

2-6 الأعمدة والمسافة

المصطلحات والرموز

القسم الثاني

الفصل3: المثلثات المتطابقة

التهيئة للفصل 3

3-1 تصنيف المثلثات

استكشاف 2-3 زوايا المثلثات

3-2 زوايا المثلثات

3-3 المثلثات المتطابقة

3-4 إثبات تطابق المثلثات SAS, SSS

3-5 إثبات تطابق المثلثات AAS, ASA

توسع 5-3 تطابق المثلثات القائمة

3-6 المثلثات المتطابقة الضلعين والمثلثات المتطابقة الأضلاع

3-7 المثلثات والبرهان الإحداثي

الفصل4: العلاقات في المثلث

التهيئة للفصل 4

استكشاف 1-4 إنشاء المنصفات

4-1 المنصفات في المثلث

استكشاف 2-4 إنشاء القطع المتوسطة والارتفاعات

4-2 القطع المتوسطة والارتفاعات في المثلث

4-3 المتباينات في المثلث

4-4 البرهان غير المباشر

استكشاف 5-4 متباينة المثلث

4-5 متباينة المثلث

4-6 المتباينات في مثلثين

الفصل5: الأشكال الرباعية

التهيئة للفصل 5

5-1 زوايا المضلع

توسع 5-1 معمل الجداول الإلكترونية زوايا المضلع

5-2 متوازي الأضلاع

5-3 تمييز متوازي الأضلاع

5-4 المستطيل

5-5 المعين والمربع

5-6 شبه المنحرف وشكل الطائرة الورقية

الرموز والمصطلحات

القسم الثالث

الفصل 6: التشابه

التهيئة للفصل 6

6-1 المضلعات المتشابهة

6-2 المثلثات المتشابهة

6-3 المستقيمات المتوازية والأجزاء المتناسبة

6-4 عناصر المثلثات المتشابهة

توسع 4-6 معمل الهندسة: الكسريات

الفصل 7: التحويلات الهندسية والتماثل

التهيئة للفصل 7

7-1 الانعكاس

7-2 الإزاحة (الانسحاب)

استكشاف 3-7 معمل الهندسة: الدوران

7-3 الدوران

استكشاف 4-7 معمل الحاسبة البيانية: تركيب التحويلات الهندسية

7-4 تركيب التحويلات الهندسية

توسع 4-7 معمل الهندسة: التبليط

7-5 التماثل

7-6 التمدد

الفصل 8: الدائرة

التهيئة للفصل 8

8-1 الدائرة ومحيطها

8-2 قياس الزوايا والأقواس

8-3 الأقواس والأوتار

8-4 الزوايا المحيطية

8-5 المماسات

8-6 القاطع والمماس وقياسات الزوايا

8-7 قطع مستقيمة خاصة في الدائرة

استكشاف 8-8 معمل الحاسبة البيانية: معادلة الدائرة

8-8 معادلة الدائرة

المصطلحات والرموز

كتاب النشاط

نشاط الفصل 1: التبرير والبرهان

1-1 التبرير الاستقرائي والتخمين

1-2 المنطق

1-3 العبارات الشرطية

1-4 التبرير الاستنتاجي

1-5 المسلمات والبراهين الحرة

1-6 البرهان الجبري

1-7 إثبات علاقات بين القطع المستقيمة

1-8 إثبات علاقات بين الزوايا

نشاط الفصل 2: التوازي والتعامد

2-1 المستقيمان والقاطع

2-2 الزوايا والمستقيمات المتوازية

2-3 إثبات توازي مستقيمين

2-4 ميل المستقيم

2-5 صيغ معادلة المستقيم

2-6 الأعمدة والمسافة

نشاط الفصل 3: المثلثات المتطابقة

3-1 تصنيف المثلثات

3-2 زوايا المثلثات

3-3 المثلثات المتطابقة

3-4 إثبات تطابق المثلثات SAS, SSS

3-5 إثبات تطابق المثلثات AAS, ASA

3-6 المثلثات المتطابقة الضلعين والمثلثات المتطابقة الأضلاع

3-7 المثلثات والبرهان الإحداثي

نشاط الفصل 4: العلاقات في المثلث

4-1 المنصفات في المثلث

4-2 القطع المتوسطة والارتفاعات في المثلث

4-3 المتباينات في المثلث

4-4 البرهان غير المباشر

4-5 متباينة المثلث

4-6 المتباينات في مثلثين

نشاط الفصل 5: الأشكال الرباعية

1-1 زوايا المضلع

1-2 متوازي الأضلاع

1-3 تمييز متوازي الأضلاع

1-4 المستطيل

1-5 المعين والمربع

1-6 شبه المنحرف وشكل الطائرة الورقية

نشاط الفصل 6: التشابه

2-1 المضلعات المتشابهة

2-2 المثلثات المتشابهة

2-3 المستقيمات المتوازية والأجزاء المتناسبة

2-4 عناصر المثلثات المتشابهة

نشاط الفصل 7: التحويلات الهندسية والتماثل

3-1 الانعكاس

3-2 الإزاحة (الانسحاب)

3-3 الدوران

3-4 تركيب التحويلات الهندسية

3-5 التماثل

3-6 التمدد

نشاط الفصل 8: الدائرة

4-1 الدائرة ومحيطها

4-2 قياس الزوايا والأقواس

4-3 الأقواس والأوتار

4-4 الزوايا المحيطية

4-5 المماسات

4-6 القاطع والمماس وقياسات الزوايا

4-7 قطع مستقيمة خاصة في الدائرة

4-8 معادلة الدائرة

2-4 ميل المستقيم

ميل المستقيم

إيجاد ميل المستقيم

أجد ميل المستقيم أستعمل الميل لتحديد المستقيمات المتوازية والمستقيمات المتعامدة

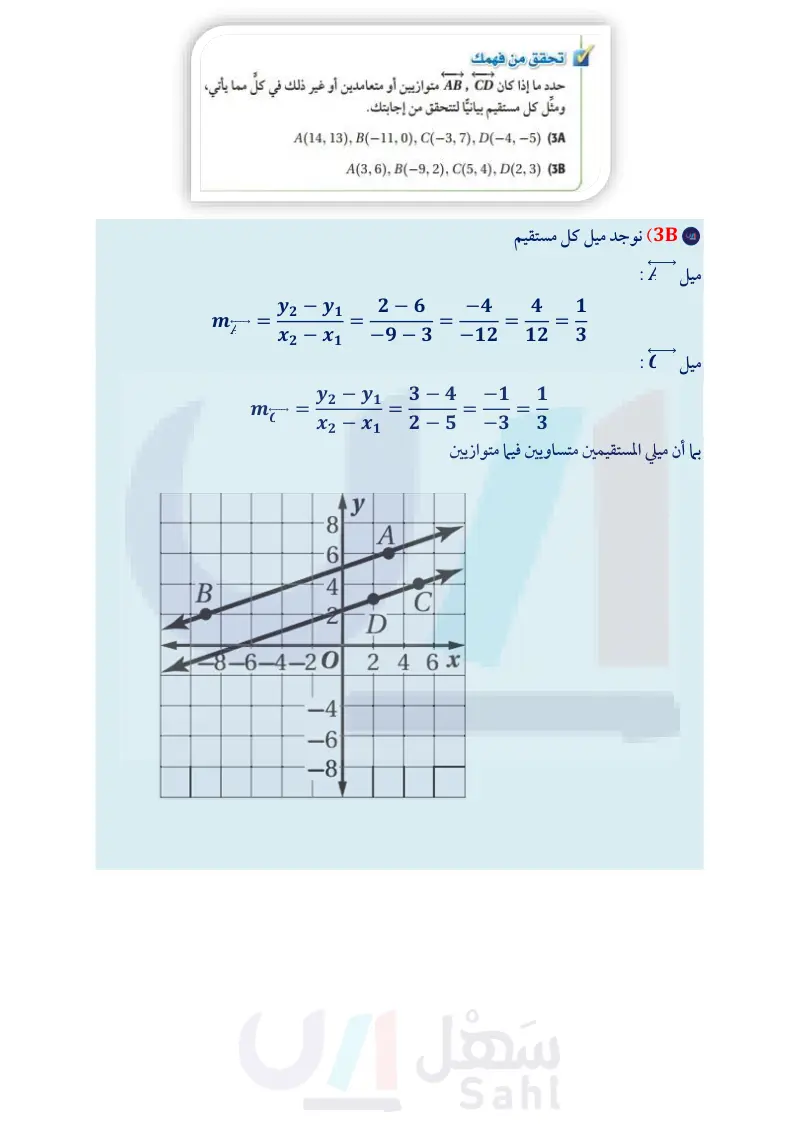
2-4 ميل المستقيم

b)إيجاد ميل المستقيم

أربع حالات مختلفة للميل

أوجد ميل كل مستقيم فيما يأتي المستقيم الذي يحتوي على (-5, -3) , (-2, 6)

القسمة على 0

2-4 ميل المستقيم

استعمال الميل معدلاً للتغير

فكم تكون مبيعاته من العلب عام 2020م ؟

المسارات الجوية

2-4 ميل المستقيم

المستقيمات المتوازية والمستقيمات المتعامدة

تحديد علاقات المستقيمات

حدد ما إذا كان CD, AB متوازيين أو متعامديين أو غير ذلك في كل مما يأتي

ميلا المستقيمين المتعامدين

2-4 ميل المستقيم

استعمال الميل لتمثيل المستقيم بيانياً

تأكد أوجد ميل كل مستقيم فيما يأتي

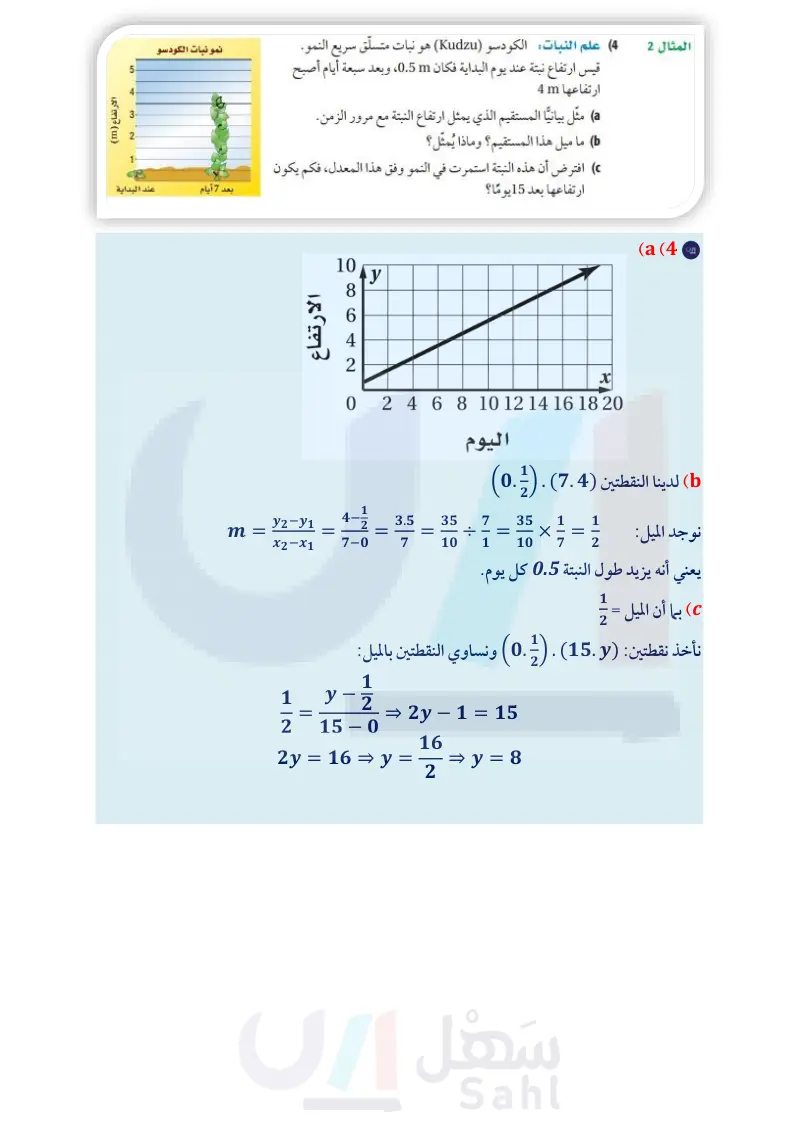
مثل بيانياً المستقيم الذي يمثل ارتفاع النبتة مع مرور الزمن

حدد ما إذا كان WX , YZ متوازيين أو متعامدين او غير ذلك في كل مما يأتي

مثل بيانياً المستقيم الذي يحقق الشروط في كل مما يأتي

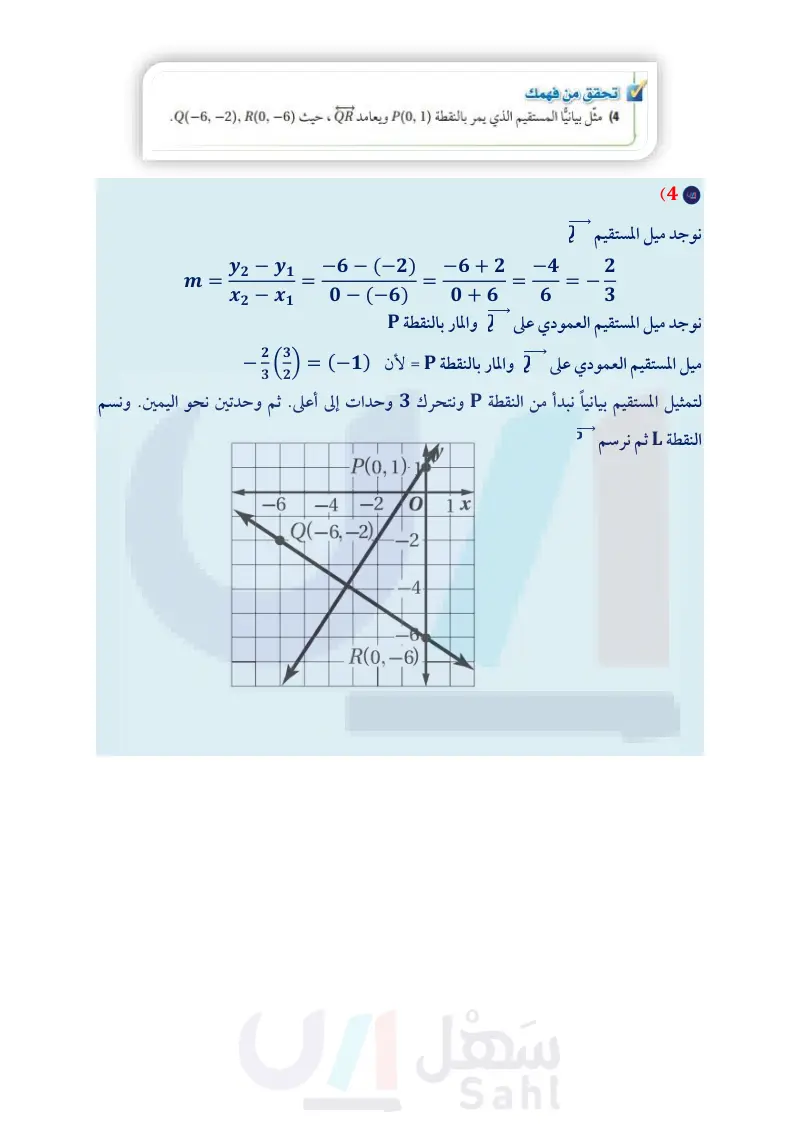
مثل بيانيا المستقيم الذي يمر بالنقطة p(0.1) ويعامد QR

2-4 ميل المستقيم

تدرب أوجد ميل كل مستقيم فيما يأتي

ارسم مستقيماً يمثل توقعاً لسعر الحاسوب الحاسوب للسنوات من 1435 هـ إلى 1439 هـ

تدرب حدد ما إذا كان CD, AB متوازيين أو متعامديين أو غير ذلك في كل مما يأتي

مثال4 مثل بيانياً المستقيم الذي يحقق الشروط في كل مما يأتي

أوجد ميل المستقيم الذي يمر بالنقطتين المحددتين في كل مما يأتي

ما المعدل التقريبي لتغير عدد سكان هذه المدينة من عام 1427هـ إلى 1439هـ؟

2-4 ميل المستقيم

حدد أي المستقيمين في السؤالين له أكبر ميل

حسب كل من خالد وطارق ميل المستقيم الذي يمر بالنقطتين هل إجابة أي منهما صحيحة؟ وضح تبريرك

أوجد معدل التغير لعدد حيوانات المها العربي في المحمية

أوجد قيمة x أو y اعتمادا على المعطيات في كل مما يأتي، ثم مثل المستقيم بيانيا

كم يصبح عدد طلاب مدرسة الاندلس عام 1440 هـ؟

أوجد الرأسين الآخرين B D للمربع

تبذل المملكة جهودا حديثة للحفاظ على البيئة بعناصرها المختلفة، حيث أسست الهيئة السعودية للحياة الفطرية

2-4 ميل المستقيم

صف ميل كل من برج المملكة وبرج بيزا

أي المعادلات الآتية تمثل مستقيما يعامد المستقيم الذي معادلتة

أوجد قياس كل من الزوايا الاتية

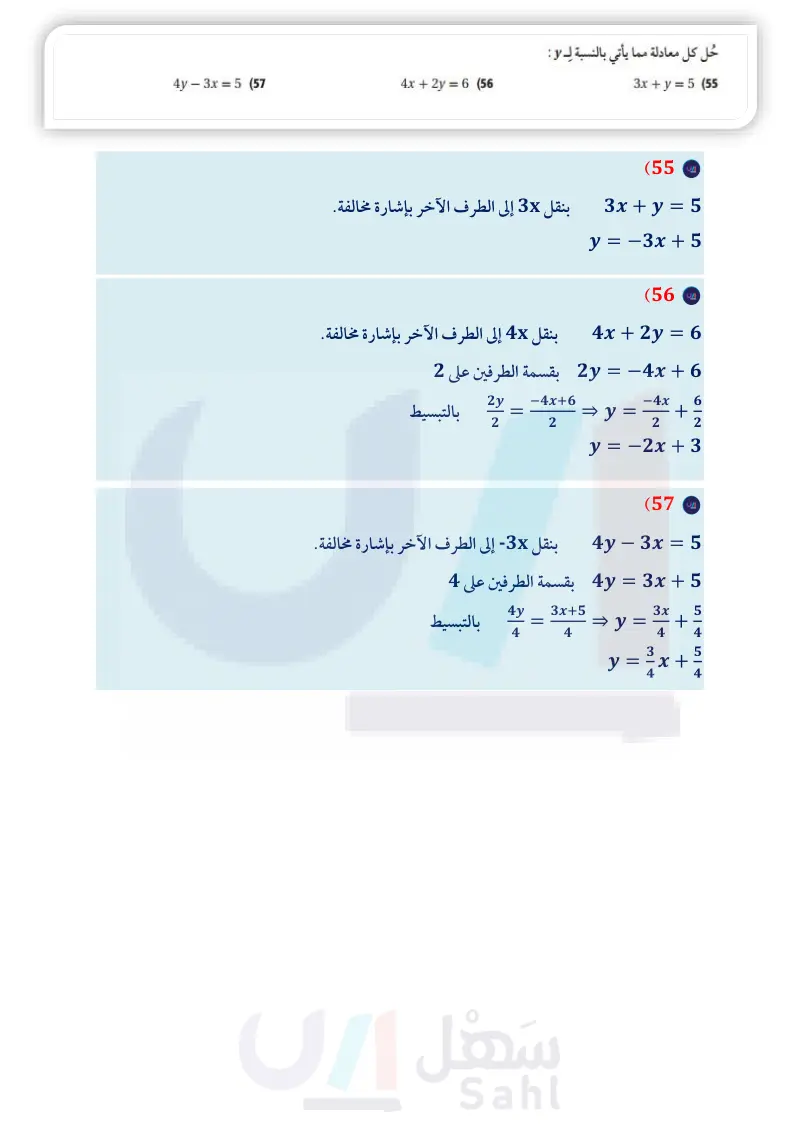
حل كل معادلة مما يأتي بالنسبة لـ y

اكتب برهانا جبريا لتبين أن يمكم ايضا حساب الميل باستعمال المعادلة

أي القيم الآتية تمثل ميل المستقيم المار بالنقطتين

حدد كلا مما يأتي مستعملا الشكل المجاور

معتمدا على المعطيات حددا ما إذا كانت النتيجة صحيحة أم لا في كل مما يأتي