استكشاف حل المعادلات والمتباينات الأسية - رياضيات1-3 - ثالث ثانوي
الفصل الأول: تحليل الدوال
الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية
نشاط الفصل الأول: تحليل الدوال
نشاط الفصل الثاني: العلاقات والدوال الأسية واللوغاريتمية
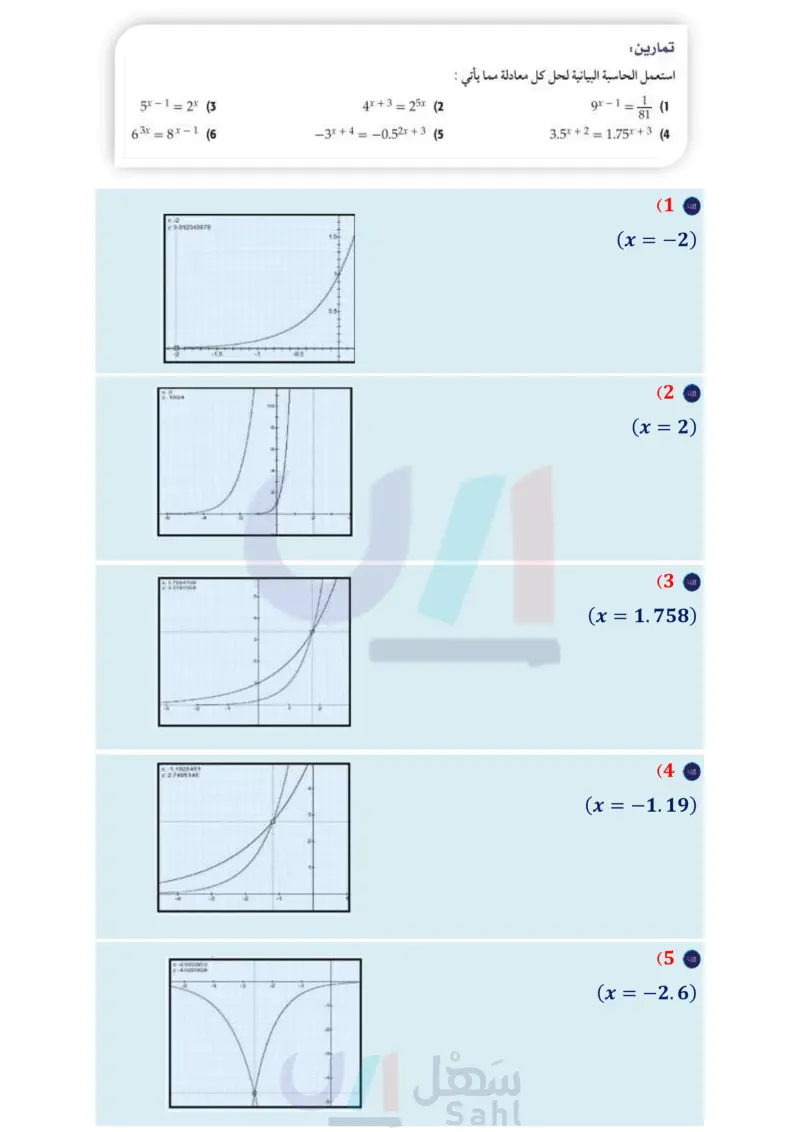
-5 رابط الدرس الرقمي www.ien.edu.sa 12(x)=1 86-1 0.5 y 0.05 2 -0.5 استكشاف معمل الحاسبة البيانية: حل المعادلات والمتباينات الأسية Solving Exponential Equations and Inequalities 1.1 f1(x)=3x-4 1.1 f1(x)=3x-4 12(x)=1 *86-1 0.5 y الحد الأقصى 12(x)=1 9 0.05 -0.5 تقاطع - 2-2 6 يمكن استعمال الحاسبة البيانية TI-nspire ، لحل المعادلات الأسية بيانيًا أو باستعمال خاصية الجدول. ولعمل ذلك اكتب المعادلات الأسية على صورة نظام من المعادلات. نشاط 1 استعمل الحاسبة البيانية لحل المعادلة 1 = 4 – ×3 الخطوة 1 : تمثيل طرفَي المعادلة بيانيا مثل طرفي المعادلة بيانيا في صورة دالتين مستقلتين، وأدخل 4 - x 3 في f1، و و في f2، ثم مثل المعادلتين بيانيا، وذلك بالضغط على المفاتيح: 6 2,0.11 *86-1 1.1 x f1(x):= 3^(x-4) f2(x):= 1/9 9 (2,0.111) 0. 0.012346 0.1111 0.05 -5 1. 0.037037 2. 0.111111 0.1111 0.1111 f1(x)=3x-4 3. 0.333333 0.1111 4. 1. 5 3 0.1111 01111 -0.5 وزارة التعليم Ministry of Education 2024-1446 on 3x-4 enter tab enter 9 الخطوة 2 : استعمال ميزة نقاط التقاطع. إن ميزة نقاط التقاطع في قائمة تحليل الرسم البياني تمكنك من تقدير الزوج المرتب الذي يمثل نقطة التقاطع . واختر 6 : تحليل الرسم البياني واختر منها 4 نقاط التقاطع : menu اضغط على مفتاح اضغط في أي نقطة على الشاشة وحرّك المؤشر مرورًا بنقطة التقاطع، سيظهر الزوج المرتب (2,0.111)؛ أي أن الحل هو 2 الخطوة 3 : استعمال خاصية الجدول تستعمل هذه الخاصية عادة لإنشاء جدول لقيم الدالة ؛ يسهم في تحليلها (تحديد أصفارها، وتحديد . خطوط التقارب لها، وتحديد نقطة تقاطع دالتين .. إلخ). تحقق من صحة حلك باستعمال خاصية الجدول. اعمل جدولًا في شاشة جانبية، وذلك بالضغط menu 7 : الجدول على مفتاح واختر منها ثم اختر 1 اظهار الجدول في شاشة جانبية (Ctrl + T) يبين الجدول قيم x وقيم (f(x أو y المناظرة لها لكل تمثيل بياني؛ فعندما 2 = x ، يكون للدالتين وهي 1 9 ≈0.111 ، وهذا يعني أن حل المعادلة هو القيمة نفسها، التحقق عوّض عن x بـ 2 في المعادلة الأصلية. .2 المعادلة الأصلية بتعويض 2 بدلا من x بالتبسيط الحل صحيح 5x - 1 = 2x (3 63x=8x-1 (6 4x + 3 = 25x (2 - 3x + 4 = -0.52x + 3 (5) 3x-421 9 32-4 21 9 3-22 1 9 11 = 11/13 ✓ تمارين : استعمل الحاسبة البيانية لحل كل معادلة مما يأتي . 9x-1 1 = (1 81 3.5% +2 +3 = 1.75% (4 الفصل 2 العلاقات والدوال الأسية واللوغاريتمية 88

10 X y≤2x-2 0.5 v≤2x-2 0.5 *87-1 2 1.2 y≥(0.5)x-3 *87-1 5 1.2 1.1 y≥(0.5)x-3 (2.5, 1.41) 87-1 1.3 1.2 1.1 D y2 =2^(x-2)=(0.5)^('x- 1.5 0.707107 2.82843 2 1 2. 15 3456 2.5 1.41421 1.41421 3 2 1. 3.5 2.82843 0.707107 6 3 1.1 ✓ y>0.5*-3 هي. وبطريقة مشابهة، يمكنك استعمال الحاسبة البيانية TInspire لحل متباينات أسية. نشاط 2 استعمل الحاسبة البيانية لحل المتباينة 3 - x - 2 > 0.5 x 2 الخطوة 1 : تمثيل المتباينات المناظرة. أعد كتابة المسألة على صورة نظام من المتباينات. x- المتباينة الأولى هي : 1 - 2 - 2 أو 2 - × 2 = y ، والمتباينة الثانية ثم مثلها بالضغط على المفاتيح: on del ≤ 2x-2 enter tab del 2 0.5 x - 3 enter فتكون منطقة الحل هي منطقة التظليل المشترك. الخطوة 2 : تحديد مجموعة الحل مجموعة إحداثيات x للنقاط التي تقع في منطقة تقاطع التظليلين تمثل مجموعة الحل للمتباينة menu الأصلية، وباستعمال ميزة نقاط التقاطع وذلك بالضغط على مفتاح ، واختيار 6 : تحليل الرسم البياني ثم اختيار 4 : نقاط التقاطع والضغط في أي نقطة على الشاشة وتحريك المؤشر مرورًا بنقطة التقاطع، سيظهر الزوج المرتب (251)، حيث يمكن استنتاج أن مجموعة الحل هي .{x | x > 2.5} الخطوة 3 : استعمال تطبيق القوائم وجداول البيانات تحقق من الحل باستعمال تطبيق القوائم وجداول البيانات . أنشئ جدولا لقيم x بزيادة 0.5 في كل مرة، وذلك بالضغط على المفاتيح on ، واكتب 2 - 2x = 11 في العمود الثاني، في كل مرّة. لاحظ أنه لقيم x الأكبر من المتغير 3 - x 0.5 = 12 في العمود الثالث واختر 2.5 = x تكون 2 < 1، وهذا يؤكد أن حل المتباينة هو {2.5 = x | x} . X 3x-4≤52 (9 16 - 1 > 22x + 2 8 (8 124x - 7 < 4 2x + 3 (12 12x-5 12x - 5 > 9.32 (11 تمارين استعمل الحاسبة البيانية لحل كل متباينة مما يأتي : 62 - x - 4 - -0.25x - 2.5 (7 52+3 5x + 3 < 2x + 4 (10 ≤2x+4 13 اكتب وضح لماذا يكون تمثيل نظام من المعادلات بيانياً صالحًا لحل معادلات أو متباينات أسية. وزارة التعليم استكشاف - معمل الحاسبة البيانية: حل المعادلات والمتباينات الأسية of 89 2024-1446