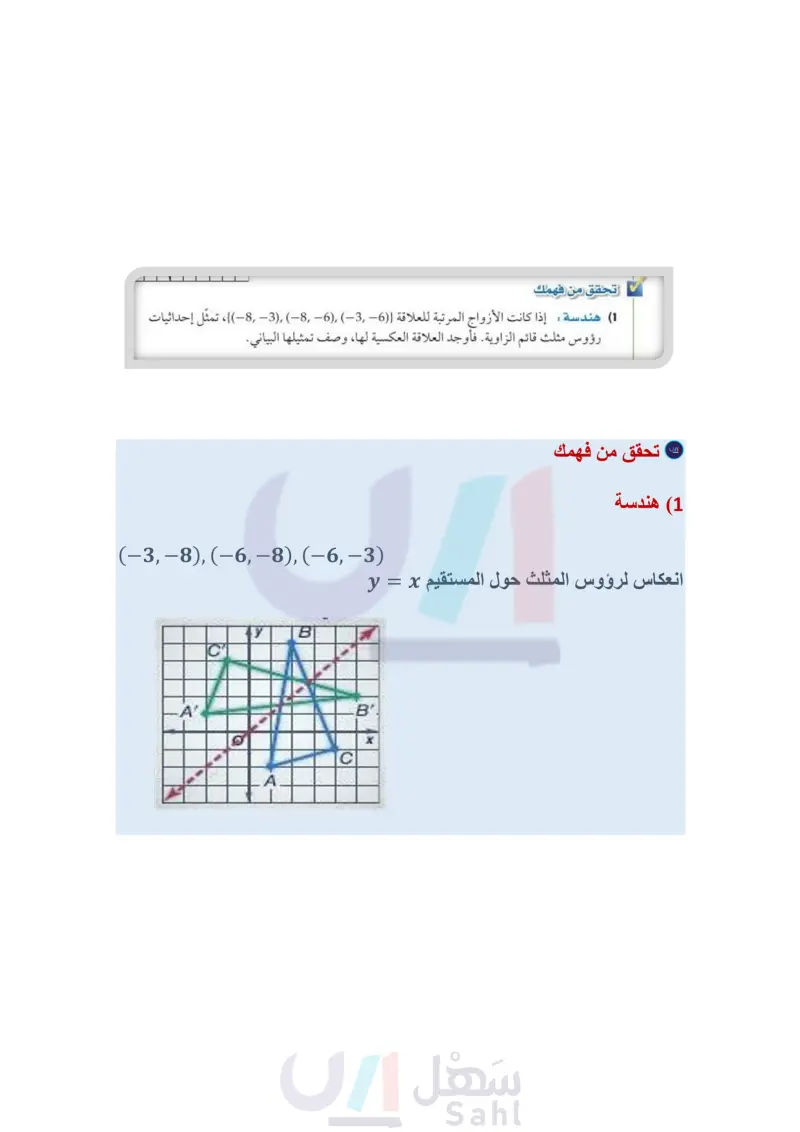
العلاقات والدوال العكسية - رياضيات2-2 - ثاني ثانوي
الفصل الرابع: العلاقات والدوال العكسية والجذرية
الفصل الخامس: العلاقات والدوال النسبية
الفصل السادس: المتتابعات والمتسلسلات
نشاط الفصل الرابع: العلاقات والدوال العكسية والجذرية
نشاط الفصل الخامس: العلاقات والدوال النسبية
www.icn.edu.sa العلاقات والدوال العكسية Inverse Functions and Relations 4-2 فيما سبق درست كتابة معادلات بالنسبة لمتغير محدد وحلها. والان . أجد كلا من العلاقة العكسية والدالة العكسية. أحدد ما إذا كانت علاقة الماذا؟ يبين الجدول المجاور قيمة الريال السعودي مقارنة بالدولار الأمريكي والدالة 7 0.267 = d تمثل عدد الدولارات التي تحصل عليها مقابل كل ريال سعودي، ولمعرفة عدد الريالات التي تحصل عليها مقابل كل دولار أمريكي، حل المعادلة السابقة بالنسبة للمتغير x فتكون النتيجة r = 3.75 d وتمثل دالة عكسية للدالة السابقة . السعودية أمريكا السعودية أمريكا 0.267 3.75 أو دالة) تمثل علاقة إيجاد العلاقة العكسية : تذكّر أن العلاقة هي مجموعة من الأزواج المرتبة والعلاقة العكسية هي مجموعة عكسية أو دالة عكسية) من الأزواج المرتبة، يمكنك الحصول عليها عن طريق تبديل إحداثيات كل زوج مرتب في العلاقة، فيصبح مجال لأخرى أم لا. المفردات العلاقة العكسية العلاقة هو مدى العلاقة العكسية لها، ومداها هو مجال العلاقة العكسية لها. مفهوم أساسي العلاقة العكسية أضف إلى لويتك التعبير اللفظي: تكون كل من العلاقتين عكسية للأخرى إذا وفقط إذا تحقق الشرط التالي كلما احتوت إحداهما على زوج مرتب (ab) احتوت الأخرى على الزوج المرتب (b). مثال: كل من العلاقتين A,B علاقة عكسية للأخرى : A' A = {(1, 5), (2, 6), (3,7)} B={(5, 1), (6, 2), (7, 3)} مثال 1 إيجاد العلاقة العكسية هندسة يمكن تمثيل رؤوس ABC بالعلاقة (41) ,(2,5) ,(2 - 1). أوجد العلاقة العكسية لها، ثم مثل بيانيًّا العلاقة والعلاقة العكسية لها على مستوى إحداثي واحد، واذكر التحويل الهندسي الذي يحوّل العلاقة المعطاة إلى العلاقة العكسية لها. مثل العلاقة بيانيا. ولإيجاد العلاقة العكسية قم بتبديل إحداثيات الأزواج المرتبة. فتكون العلاقة العكسية هي : ()()(2). وبتمثيل هذه الأزواج المرتبة للعلاقة العكسية بيانيًا يتضح أنها تمثل رؤوس 'AA'B'C بعد انعکاس رؤوس AABC حول المستقيم y = x. R B C x C A σ تحقق من فهمك 1) هندسة : إذا كانت الأزواج المرتبة للعلاقة (36) (8) (83)، تمثل إحداثيات رؤوس مثلث قائم الزاوية. فأوجد العلاقة العكسية لها، وصف تمثيلها البياني. إن ما ينطبق على الأزواج المرتبة في العلاقة والعلاقة العكسية، ينطبق أيضًا على الأزواج المرتبة في الدالة ومعكوسها، وإذا كان معكوس الدالة يمثل دالة أيضًا، فإنه يسمى دالة عكسية. ويرمز إلى الدالة العكسية للدالة (f(x بالرمز (f(x وزارة التعليم 19 2024-1446 الدرس 2-4 العلاقات والدوال العكسية inverse relation الدالة العكسية inverse function

مفهوم أساسي خواص الدالة العكسية التعبير اللفظي: إذا كان كل من 1, دالة عكسية للأخرى، فإن f(a) = b إذا وفقط إذا كان f-1 (b) = a. لیکن 4 - f(x) = x) ودالتها العكسية هي 4 + x) = x) . مثال: قراءة الرياضيات الدالة العكسية أوجد (6)f. أوجد (2) 1-f. أضف إلى 1- يقرأ الدالة العكسية للدالة أ. تذكر أن (1) ليس أسا. f(x)=x-4 f(6)=6-4=2 f-1(x)=x+4 f-1 (2) = 2 + 4 = 6 وبما أن كلا من ( x ) دالة عكسية للأخرى، فإن 6 = (2) 1-f ,2 = (6) . اختبار الخط الأفقي إذا كان معكوس دالة يمثل دالة أيضًا، فإن الدالة الأصلية تكون دالة متباينة. تذكر أنه يمكنك استعمال اختبار الخط الرأسي لمعرفة ما إذا كانت العلاقة تمثل دالة أم لا. وبالمثل يمكنك استعمال اختبار الخط الأفقي لتحديد ما إذا كان معكوس دالة يمثل دالة أم لا. ° | y= f(x) y= g(x) لله لا يمكن رسم أي مستقيم أفقي يقطع منحنى الدالة في أكثر من نقطة (الدالة متباينة)؛ لذا يمثل معكوس الدالة (y = f(x دالة أيضًا. يمكنك إيجاد معكوس دالة بالتبديل بين x و y في قاعدة الدالة. مثال 2 يمكن رسم مستقيم أفقي يقطع منحنى الدالة، في أكثر من نقطة ( الدالة ليست متباينة)؛ لذا لا يكون معكوس الدالة (y = (x دالة. إيجاد معكوس الدالة وتمثيله بيانيا أوجد معكوس كل من الدالتين الآتيتين، ثم مثل الدالة ومعكوسها بيانيًا على مستوى إحداثي واحد. f(x) = 2x - 5 (a الخطوة 1: أعد كتابة الدالة كمعادلة بدلالة المتغيرين x, y f(x) = 2x - 5 - y = 2x - 5 الخطوة 2: بدل بين كل من المتغير x والمتغير لا في ا المعادلة 5 - x = 2y إرشادات للدراسة الخطوة 3 حل المعادلة بالنسبة للمتغير لا. رمز الدالة العكسية x = 2y - 5 x + 5 = 2y x +5 = y أضف 5 للطرفين بما أن معكوس الدالة (f(x في الفرع 4 من المثال 2 هو دالة أيضًا، لذا تم التعبير عنها .f¹(x) اقسم الطرفين على 2 الخطوة 4: ضع (x) 1- بدلا من المتغير ، إذا كان المعكوس دالة. بما أن الدالة (f(x خطية، وباستعمال اختبار الخط الأفقي، تجد أن معکوسها هو دالة أيضًا، لذا يمكنك استعمال الرمز (f-1 (x =x+5f-1(x) = x+5 y = ƒ-1(x) = x+5 فتكون الدالة العكسية للدالة 5 - f(x) = 2x هي 2 والتمثيل البياني للدالة 5 = (f(x هي انعكاس للتمثيل x+5 البياني للدالة 5 - f(x) = 2x حول المستقيم y = x. 20 الفصل 4 العلاقات والدوال العكسية والجذرية f(x)=x+5 f(x)=2x-5 0 x وزارة التعليم Ministry of Education 2024-1446

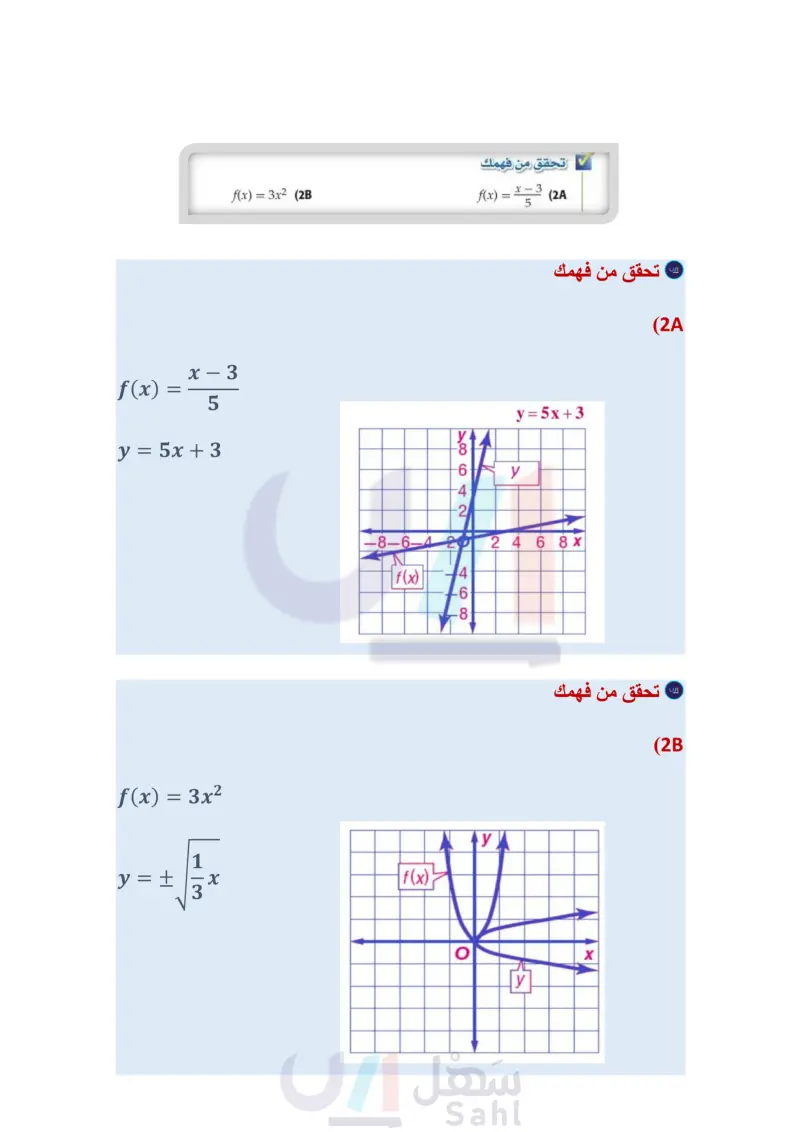
f(x) = x2 + 1 (b الخطوة 1: ارشادات للدراسة. الخطوة 2 : الدوال الخطوة 3 : معكوس الدالة أ في الفرع 6 لا يمثل دالة لأنه لا يحقق اختبار الخط الرأسي، أو لأن الدالة ا لا تحقق اختبار الخط الأفقي. تنبيه ! الدالة العكسية تأكد أن التركيبين [fog](x), [gof](x) يساوي كل منهما الدالة المحايدة x) = X) وذلك لتكون كل من الدالتين دالة عكسية للأخرى. الخطوة 4: f(x) = x2 + 1 → y = x2 + 1 x = y2 + 1 x = y2 + 1 اطرح 1 من كلا الطرفين خذ الجذر التربيعي للطرفين x - 1 = 12 Vx - 1 = y y = + Vx - 1 مثل بيانيا 1 - y = Vx بإجراء انعكاس لمنحنى الدالة 1 + f(x) = x2 حول المستقيم y = x. تحقق من فهمك f(x) = x=³ (2A f(x)=3x² (2B y=tvx - |f(x)=x²+ 0 التأكد من الدالة العكسية يمكنك تحديد ما إذا كانت دالتان، كل منهما تمثل دالة عكسية للأخرى أم لا، وذلك بإيجاد كل من تركيبيهما. مفهوم أساسي الدالة العكسية التعبير اللفظي: تكون كلٌّ من الدالتين 9, f دالة عكسية للأخرى، إذا وفقط إذا كان تركيب الرموز كل منهما يساوي الدالة المحايدة (x) = (x) الدالتان ( x ) ( كل منهما تمثل دالة عكسية للأخرى، إذا وفقط إذا كان [g of](x) = [fog](x) = x مثال 3 التأكد أن كل دالة تمثل دالة عكسية للأخرى في كل زوج مما يأتي حدد هل كل دالة تمثل دالة عكسية للأخرى أم لا؟ ووضّح إجابتك. f(x)=3x+9, g(x)=x -3 (a تأكد بأن تركيب الدالتين (f(x) (x يساوي الدالة المحايدة. [fg](x) = f[g(x)] = f ( x − 3) - +9 =3(x-3) + = x - 9 + 9 = x [g of](x) = g[f(x)] = g(3x+9) = 1/1(3x + +9) 3 = x + 3 - 3 = x إذن تمثل كلّ من الدالتين دالة عكسية للأخرى؛ لأن fo g](x) = [g of(x) = x] f(x)=4x², g(x)=2√√x (b [fog](x)=flg(x)] = f(2√x) =4(2√x)² = 4(4x) = 16x بما أن fox) x] ، فإن الدالتين (x) و (f(x لا تمثل كلٌّ منهما دالة عكسية للأخرى تحقق من فهمك f(x)=3x-3, g(x) = x + 4 (3A x+1 ±1 (3B f(x)=2x³-1, g(x) = · أضف إلى نك وزارة التعليم الدرس 2-4 العلاقات والدوال العكسية 21 2024-1446

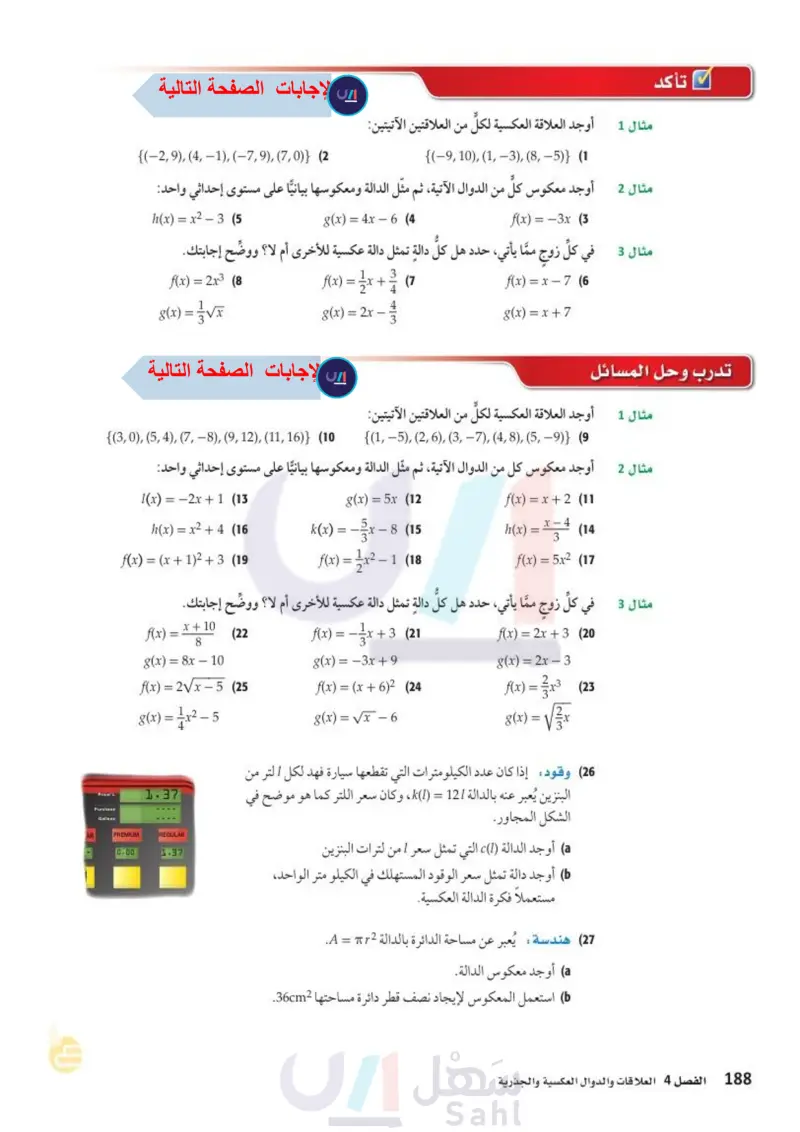
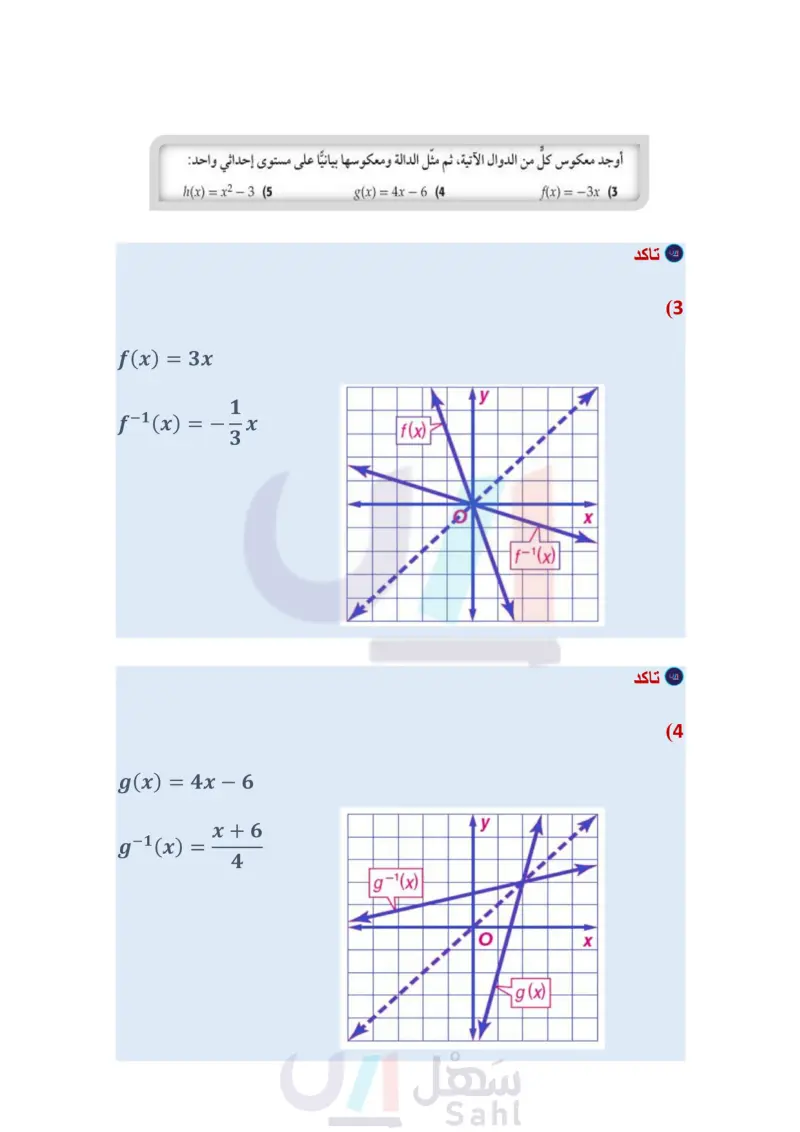
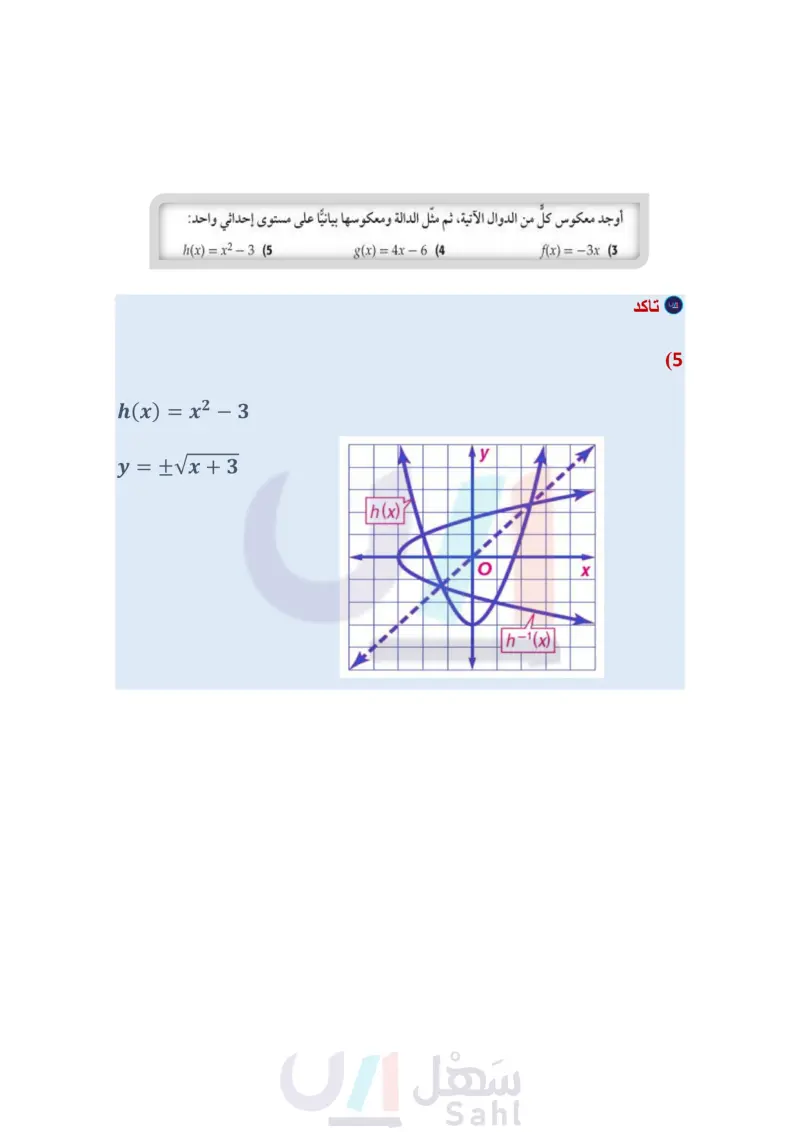
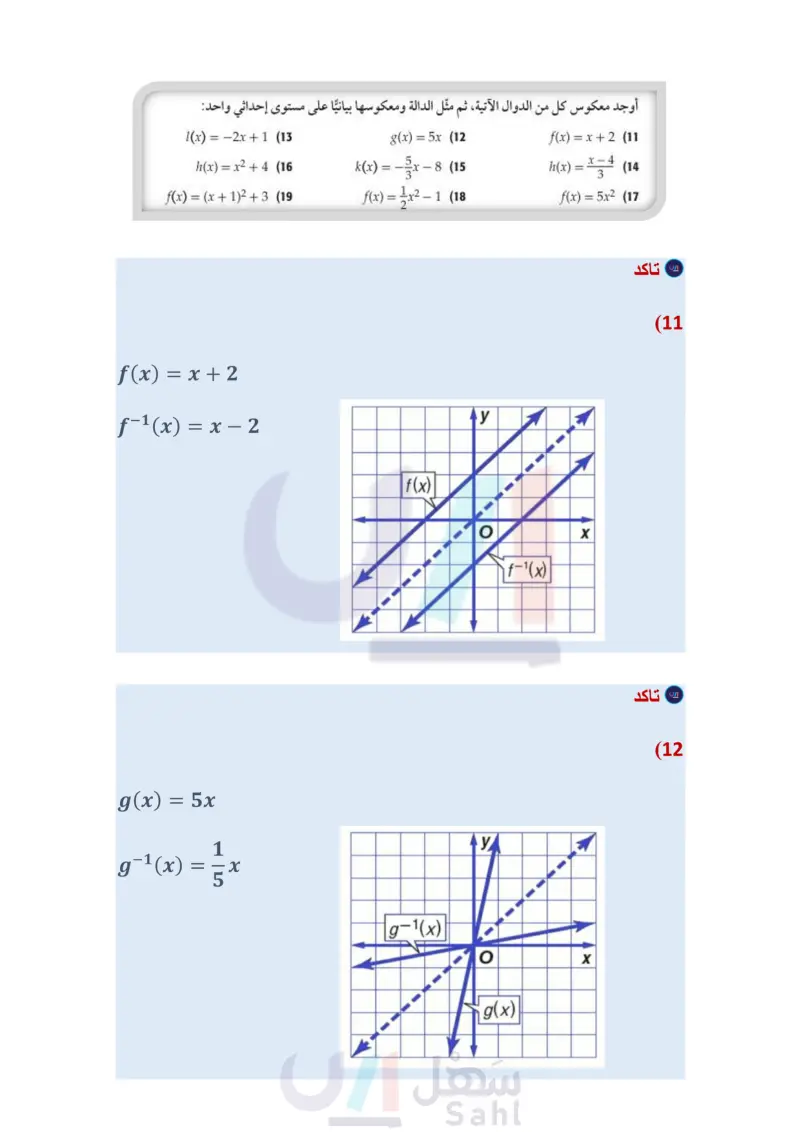
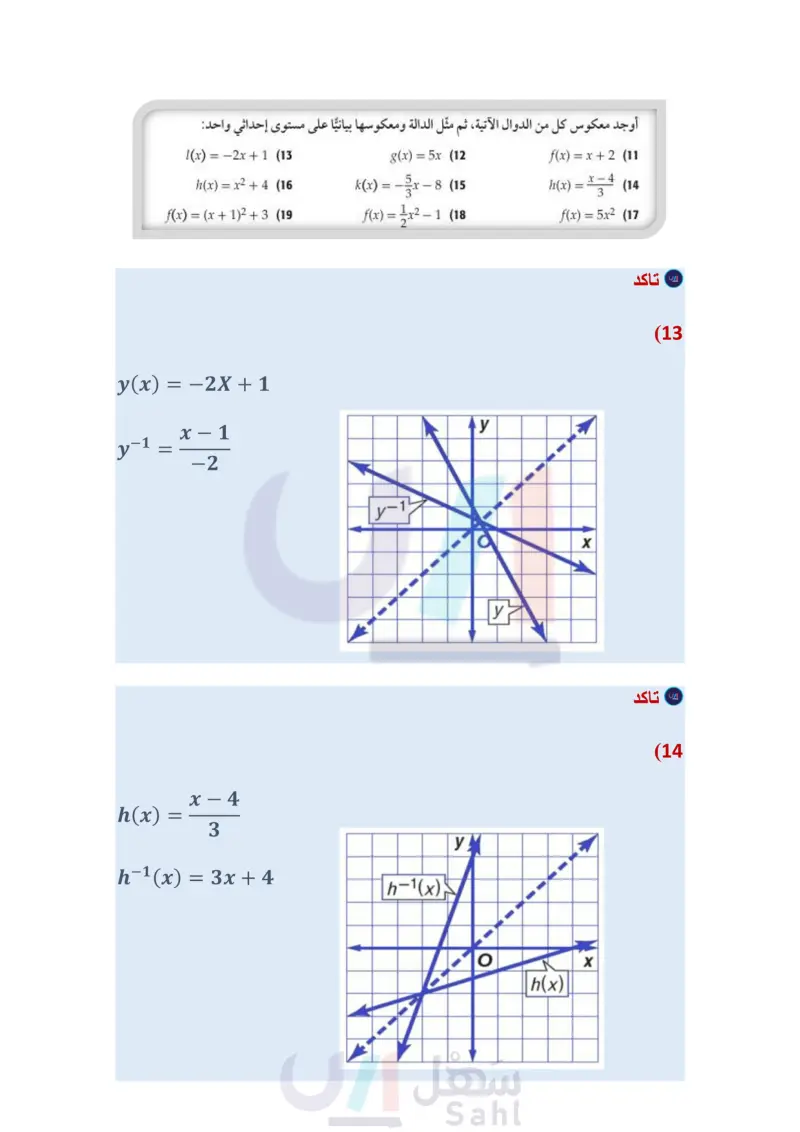
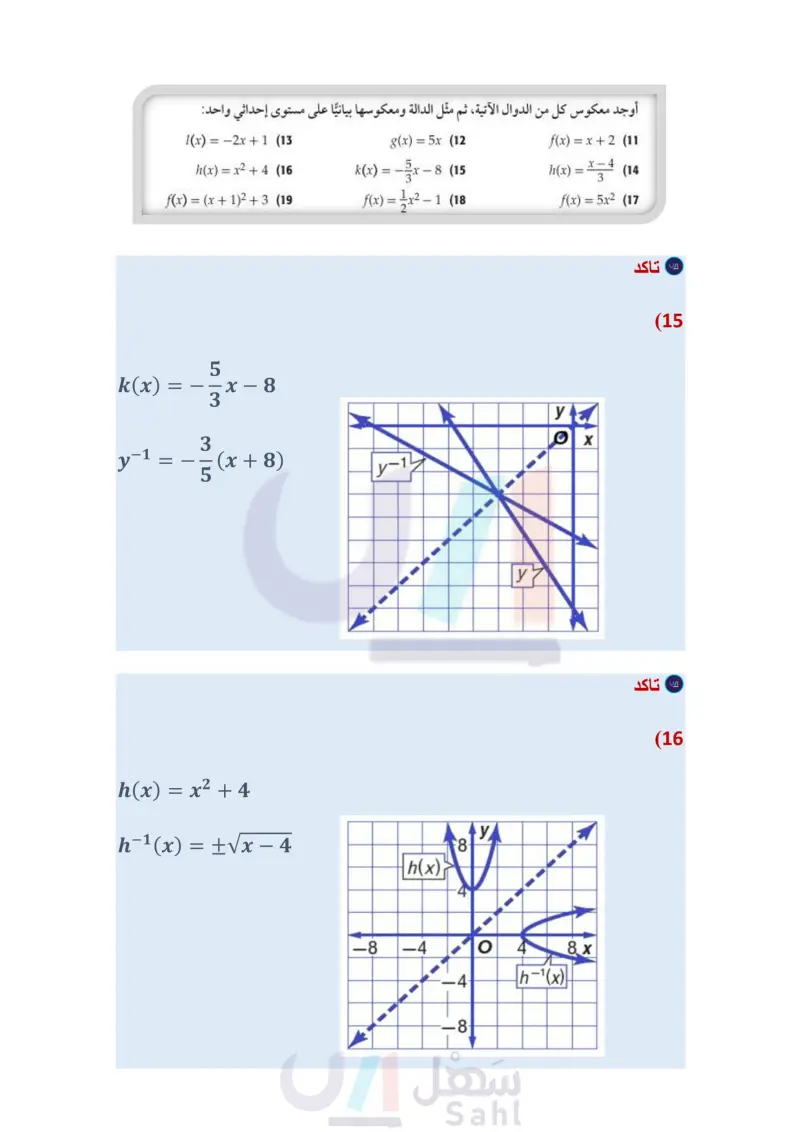
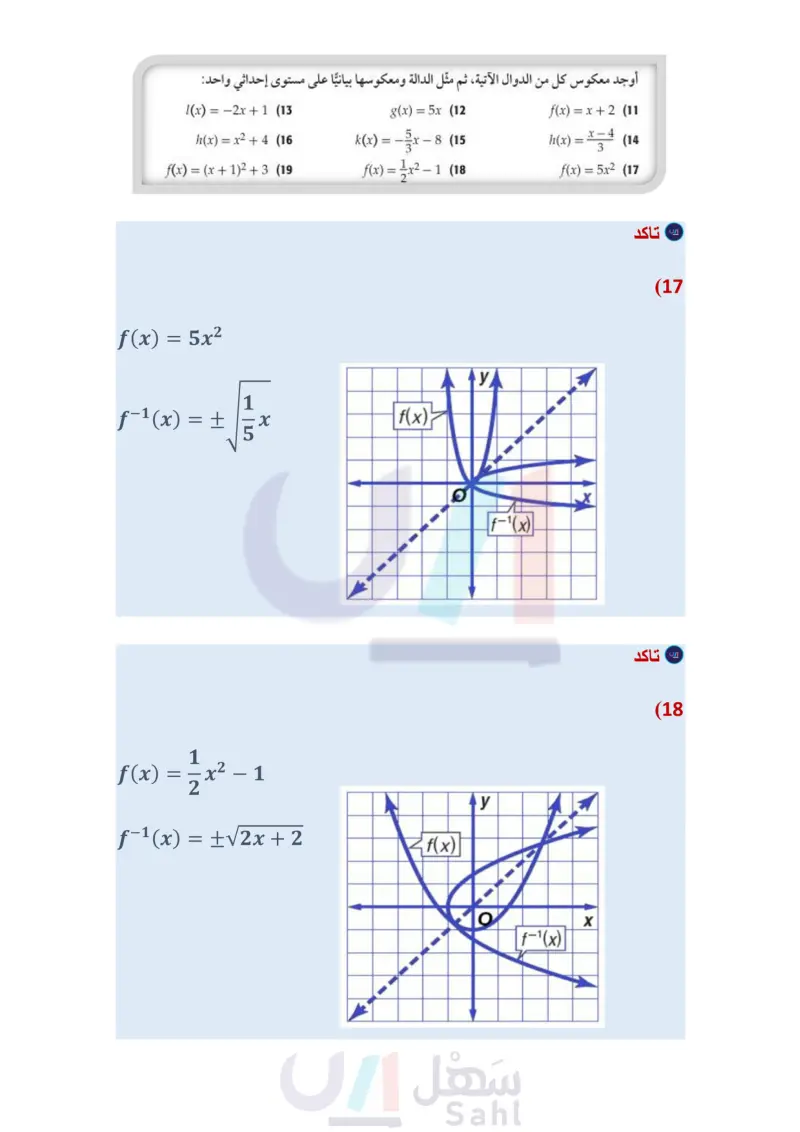
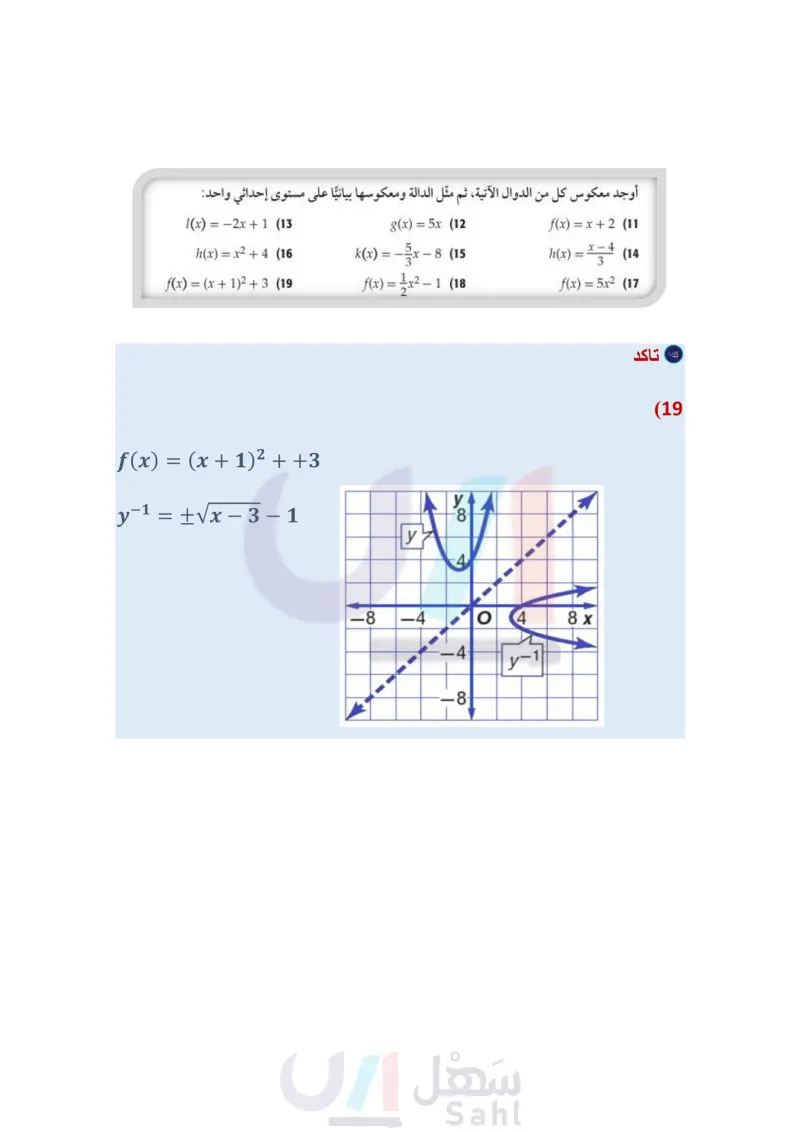
تأكد مثال 1 أوجد العلاقة العكسية لكل من العلاقتين الآتيتين: {(-9, 10), (1,3), (8,-5)} (1 {(-2,9), (4, 1), (-7,9), (7,0)} (2 مثال 2 أوجد معكوس كلُّ من الدوال الآتية، ثم مثل الدالة ومعكوسها بيانيًا على مستوى إحداثي واحد: f(x)=-3x (3 g(x)=4x-6(4 h(x) = x²-3 (5 مثال 3 في كل زوج مما يأتي، حدد هل كلُّ دالة تمثل دالة عكسية للأخرى أم لا؟ ووضّح إجابتك. f(x)=2x³ (8 8(x)=√√x f(x)=x+(7 g(x)=2x- f(x)=x-7 (6 g(x)=x+7 تدرب وحل المسائل مثال 1 أوجد العلاقة العكسية لكلّ من العلاقتين الآتيتين: {(3,0), (5, 4), (7,8), (9, 12), (11, 16)} (10 {(1, 5), (2,6), (3, -7), (4,8), (5,-9)} (9 مثال 2 أوجد معكوس كل من الدوال الآتية، ثم مثل الدالة ومعكوسها بيانيًا على مستوى إحداثي واحد: Price/L (x) = -2x + 1 (13) g(x)=5x (12 f(x) = x + 2 (11 (x) = x2 + 4 (16) f(x) = (x + 12 + 3 (19) k(x) = f(x) = x²- -8 (15 h(x) = x (14 -1 (18 f(x) = 5x2 (17 Purchase Gallons وزارة التعليم Ministry of Education 2024-1446 مثال في كل زوج مما يأتي، حدد هل كلُّ دالة تمثل دالة عكسية للأخرى أم لا؟ ووضّح إجابتك. f(x) = 1 + 10 8 (22 g(x)=8x-10 f(x)=2√√x-5 (25 8(x) = x²-5 1.37 PREMIUM 0.00 REGULAR 1.37 f(x) = : x + 3 (21 g(x)=-3x+9 f(x) = 2x + 3 (20) g(x)=2x-3 f(x)=(x+6)2 (24 f(x) = x³ (23 g(x)=√x-6 g(x) = (26) وقود إذا كان عدد الكيلومترات التي تقطعها سيارة فهد لكل 1 لتر من البنزين يُعبر عنه بالدالة 121 = ) ، وكان سعر اللتر كما هو موضح في الشكل المجاور. ) أوجد الدالة ) التي تمثل سعر 1 من لترات البنزين أوجد دالة تمثل سعر الوقود المستهلك في الكيلو متر الواحد، مستعملاً فكرة الدالة العكسية. (27) هندسة: يُعبر عن مساحة الدائرة بالدالة A = Tr2. ) أوجد معكوس الدالة. استعمل المعكوس لإيجاد نصف قطر دائرة مساحتها 36cm2. الفصل 4 العلاقات والدوال العكسية والجذرية 22 22

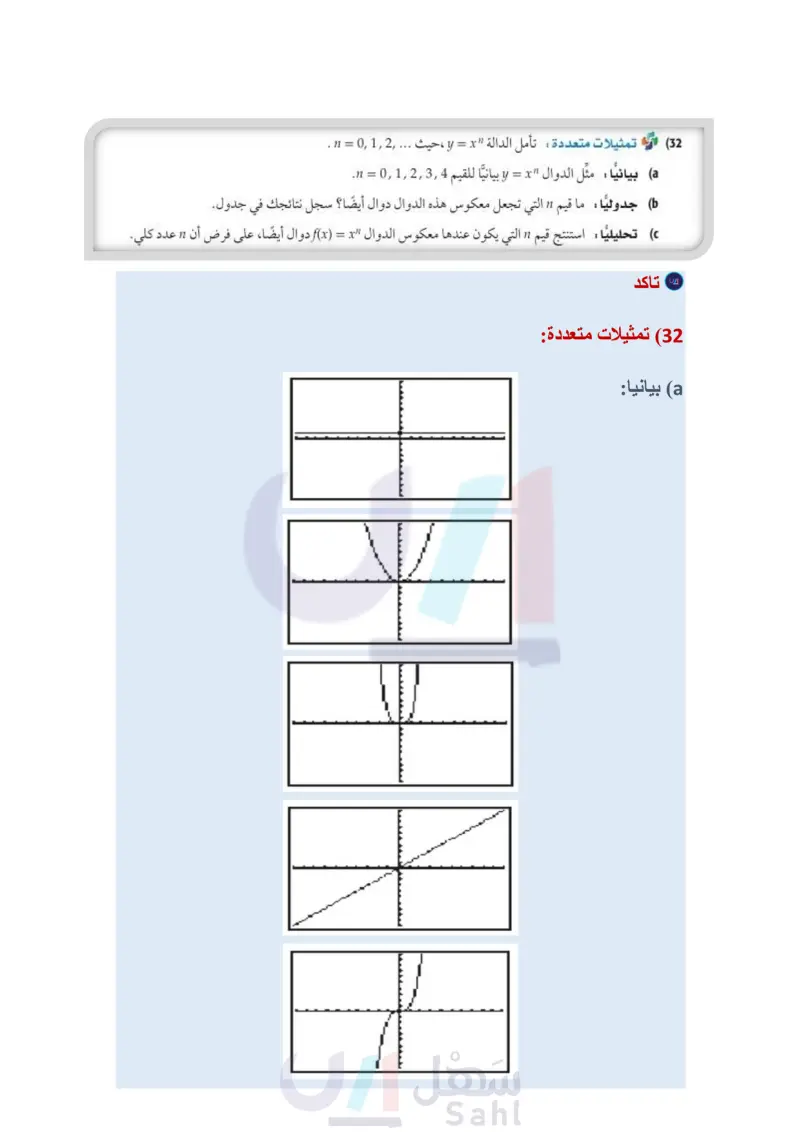
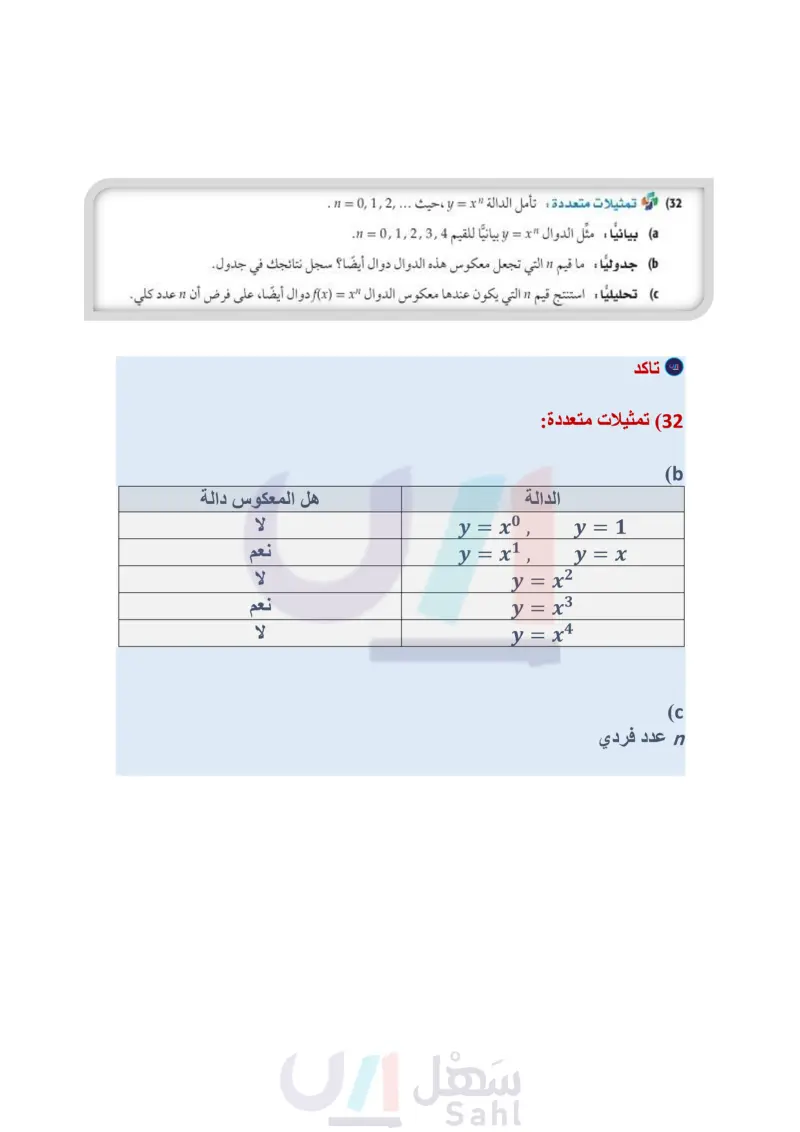
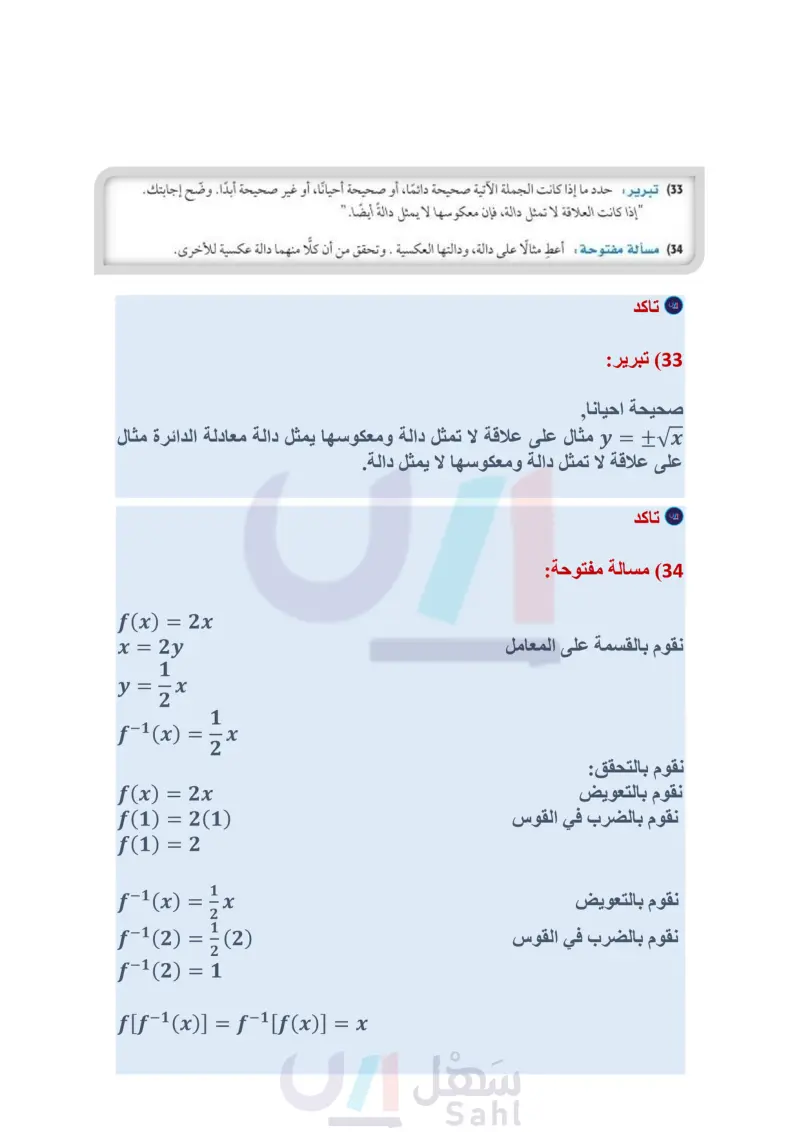
تدريب على اختبار استعمل اختبار الخط الأفقي لتحدد ما إذا كان معكوس كلَّ دالة من الدوال الآتية دالة أيضًا أم لا: f(x) = x3 - 8 (28) h(x) = 2x² (29 g(x)=3x+7 (30 31 درجات الحرارة تستعمل الصيغة 32 + F(x) = x للتحويل من درجة الحرارة السيليزية إلى درجة الحرارة الفهرنهايتية. a) أوجد (F(x. ثم بين أن (x) و (F(x تمثل كلُّ منهما دالة عكسية للأخرى. ) فيم تستعمل (F -(x ؟ (32) تمثيلات متعددة: تأمل الدالة "y = x ، حيث ... ,2 ,1 ,0 = n . بيانيا : مثل الدوال "y = x بيانيًا للقيم ! .n 0,1,2,3,4 جدوليا ما قيم " التي تجعل معكوس هذه الدوال دوال أيضًا؟ سجل نتائجك في جدول. تحليليا : استنتج قيم " التي يكون عندها معكوس الدوال f(x) = x دوال أيضًا، على فرض أن 11 عدد كلي. مسائل مهارات التفكير العليا (33) تبرير: حدد ما إذا كانت الجملة الآتية صحيحة دائمًا، أو صحيحة أحيانًا، أو غير صحيحة أبدًا. وضح إجابتك. " إذا كانت العلاقة لا تمثل دالة، فإن معكوسها لا يمثل دالة أيضًا." (34) مسألة مفتوحة: أعط مثالا على دالة، ودالتها العكسية . وتحقق من أن كلا منهما دالة عكسية للأخرى. (35) تحد: أعط مثالا على دالة معكوسها الدالة نفسها. 36 اكتب إذا كان لديك تركيب لدالتين، كل منهما دالة عكسية للأخرى. فلماذا تكون قيمة تركيب الدالتين عند العدد 5 تساوي العدد 5 دائما ؟ 3x (37) إذا كان 1 + f(x) = x2 + x = x، فأي مما يأتي يمثل 38) أي الدوال الآتية هي دالة عكسية للدالة: 5-3 = (f(x ؟ g(x)=2x+5 C 8(x)=2x-5 D 2x +5 g(x)=- x3 + x2 - 3x + 3 g(x)= 3x +5 2 B x2 - 2x + 4 D Sf[g(x)] x2 - x + 2 A -2-2 B مراجعة تراكمية إذا كان 1 - 2 x) = 3x + 5, (x) = x - 2 ) = x)، فأوجد قيمة كل مما يأتي: (الدرس: 1-4) g[f(3)] (39 f[h(-2)] (40 h[g(1)] (41 (42) مساحة: قطعة أرض على شكل شبه منحرف، طول قاعدتها الأطول يزيد بمقدار 8ft على 3 أمثال طول قاعدتها الأقصر، ويزيد ارتفاعها قدما واحدةً على 3 أمثال طول قاعدتها الأقصر. ما أبعاد قطعة الأرض إذا كانت مساحتها 4104ft2؟ (مهارة سابقة) بسط كلًا مما يأتي: (مهارة سابقة) (341)(5 2i) (43 1-i 1+1 (45 (√6+i)(√√6-i) (44 (46 1 + 2i وزارة التعليم الدرس 2-4 العلاقات والدوال العكسية 23 2024-1446




 0
0 
 0
0