الكسريات - رياضيات 1-3 - أول ثانوي

توسع 6-4 معمل الهندسة : الكسريات Fractals www.icm.edu.sa الكسريات أشكال هندسية تنتج باستعمال تكرار الأجزاء (iteration)، وتكرار الأجزاء هو عملية تكرار النمط نفسه مرّةً تلو الأخرى، وتكون الكسريات ذاتية التشابه ؛ أي أن الأجزاء الصغيرة للشكل لها الخصائص الهندسية نفسها للشكل الأصلي. انشاط 1 البداية : ارسم مثلثا متطابق الأضلاع طول المرحلة 1: صل نقاط منتصفات أضلاع المرحلة 2 كرّر العملية. المثلثات مع ضلعه 8 وحدات في ورقة منقطة. المثلث لتشكل مثلثا آخر، وظلل المثلث الثلاثة غير المظللة، وصل نقاط منتصفات الداخلي أضلاعها لتشكل ثلاثة مثلثات أخرى. إذا كرّرت هذه العملية إلى مالانهاية، فإن الشكل الناتج يسمى مثلث سير بنسكي. تحليل النتائج: 1) إذا استمررت في هذه العملية، فكم يكون عدد المثلثات غير المظللة في المرحلة 3؟ (2) ما محيط المثلث غير المظلل في المرحلة 4؟ 3) إذا استمررت في هذه العملية إلى مالانهاية، فماذا سيحصل لمحيط كل مثلث غير مظلل ؟ (4) تحد، استنادًا إلى الشكل المجاور، أكمل الآتي باستعمال برهان ذي عمودين: المعطيات: AKAP متطابق الأضلاع. ,D, E, M, B, C منتصفات: KA,AP, K, DA, F, F على الترتيب. المطلوب: ABAC ~ AKAP (5) يمكن رسم شجرة كسريّة، برسم غصنين جديدين من نهاية كل غصن أصلي، بحيث يكون طول كل غصن منها مساويًا ثلث طول الغصن السابق له . ) ارسم المرحلة 3 والمرحلة 4 للشجرة الكسرية. ما العدد الكلي للأغصان في المراحل الأربع جميعها؟ ( لا تعد الساق) اكتب عبارة جبريةً يمكن استعمالها للتنبؤ بالعدد الكلي للأغصان في نهاية كل مرحلة. 46 الفصل 6 التشابه B C Έ D F H G K L M N P المرحلة 2 المرحلة 1 وزارة التعليم Ministry of Education 2024-1446

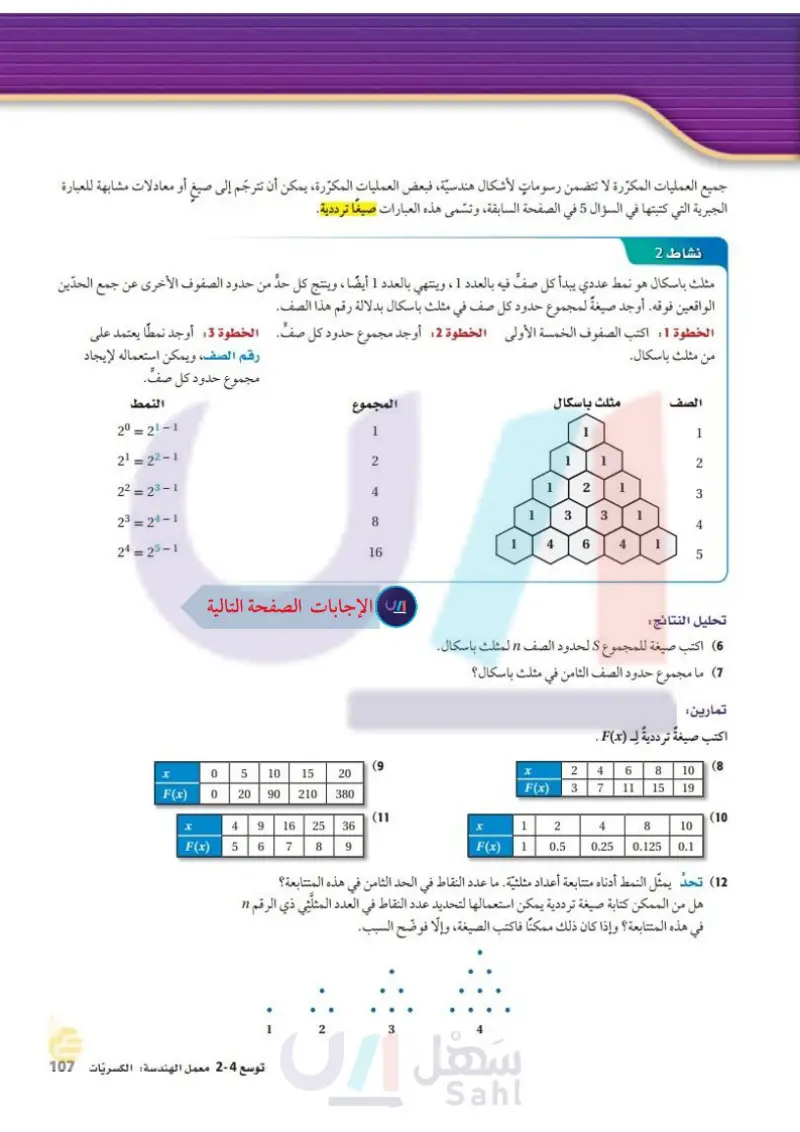
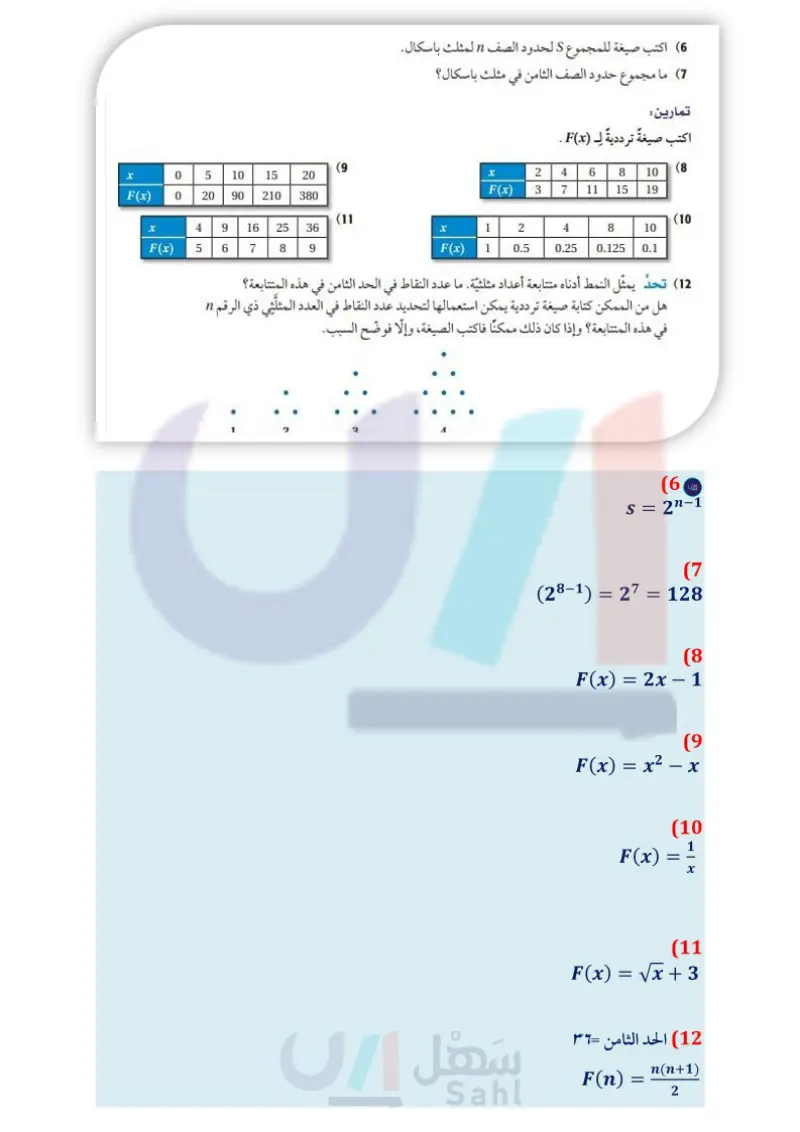
جميع العمليات المكرّرة لا تتضمن رسومات لأشكال هندسية، فبعض العمليات المكرّرة، يمكن أن تترجم إلى صيغ أو معادلات مشابهة للعبارة الجبرية التي كتبتها في السؤال 5 في الصفحة السابقة، وتسمى هذه العبارات صيفًا ترددية. نشاط 2 مثلث باسكال هو نمط عددي يبدأ كل صفّ فيه بالعدد 1، وينتهي بالعدد 1 أيضًا، وينتج كل حد من حدود الصفوف الأخرى عن جمع الحدين الواقعين فوقه أوجد صيغة لمجموع حدود كل صف في مثلث باسكال بدلالة رقم هذا الصف. الخطوة 1 اكتب الصفوف الخمسة الأولى الخطوة 2 أوجد مجموع حدود كل صف. الخطوة 3 : أوجد نمطا يعتمد على رقم الصف، ويمكن استعماله لإيجاد من مثلث باسكال. الصف مثلث باسكال المجموع مجموع حدود كل صف. النمط 20-21-1 21-22-1 1 2 1 2 22-23-1 4 3 23 - 24-1 3 3 8 4 24-25-1 6 16 5 تحليل النتائج : 6 اكتب صيغة للمجموع 5 لحدود الصف n المثلث باسكال (7) ما مجموع حدود الصف الثامن في مثلث باسكال ؟ تمارين اكتب صيغة ترددية لـ (F(x . (9 (8 0 5 10 15 20 x 2 4 8 6 10 F(x) 0 20 90 210 380 F(x) 3 7 15 11 19 (11 (10 x F(x) 49 56 16 25 36 1 2 4 8 10 8 7 9 1 F(x) 0.5 0.125 0.25 0.1 (12) تحد يمثل النمط أدناه متتابعة أعداد مثلثية. ما عدد النقاط في الحد الثامن في هذه المتتابعة؟ هل من الممكن كتابة صيغة ترددية يمكن استعمالها لتحديد عدد النقاط في العدد المثلثي ذي الرقم 1 في هذه المتتابعة؟ وإذا كان ذلك ممكنا فاكتب الصيغة، وإلا فوضح السبب. 1 2 3 توسع 4- معمل الهندسة الكسريات الت47م Ministry of Education 2024-1446

الفصـ 6 دليل الدراسة والمراجعة ملخص الفصل المفاهيم الأساسية المضلعات المتشابهة والمثلثات المتشابهة ( الدرسان 2-1-16 . يتشابه مضلعان إذا وفقط إذا كانت زواياهما المتناظرة متطابقة، وأطوال أضلاعهما المتناظرة متناسبة. . يكون المثلثان متشابهين إذا كانت AA زاويتان في أحدهما مطابقتين لزاويتين في المثلث الآخر. 555 أطوال الأضلاع المتناظرة للمثلثين متناسبة. SAS طولا ضلعين في أحدهما متناسبين مع طولي الضلعين المناظرين لهما في المثلث الآخر، والزاويتان المحصورتان متطابقتين. الأجزاء المتناسبة (الدرس (3-6) • إذا وازى مستقيم أحد أضلاع مثلث، وقطع الضلعين ا الآخرين في نقطتين محددتين، فإنه يقسم هذين الضلعين إلى قطع مستقيمة أطوالها متناسبة. مفردات أساسية المضلعات المتشابهة (ص 12) معامل التشابه (ص. (13) نسبة التشابه (ص. (13) القطعة المنصفة في المثلث (ص. 31) الكسريات (ص. 46) تكرار الأجزاء (ص 46) ذائية التشابه (ص 46) صيغة ترددية (ص. (47) اختبار المفردات a) نسبة التشابه b) معامل التشابه d) نظرية التشابه SSS نظرية التشابه SAS مسلمة التشابه AA م القطعة المنصفة اختر مما سبق رمز الجملة التي تكمل كلا مما يأتي: (1) طرفا في المثلث هما منتصفا ضلعين فيه. (2) إذا كانت : فإن ABC - AXYZ القطعة المنصفة في المثلث توازي ضلعا فيه، وطولها يساوي نصف طوله. عناصر المثلثين المتشابهين (الدرس 4-6) • إذا تشابه مثلثان فإن النسبة بين كل من طولي ارتفاعيهما المتناظرين، وطولي منصفي الزاويتين المتناظرتين، وطولي القطعتين المتوسطتين المتناظرتين تساوي النسبة بين طولي ضلعين متناظرين. المطويات منظم أفكار تأكد من أن المفاهيم الأساسية مدونة في مطويتك. المصلي النقابة وفق ؟ (3) النسبة بين طولي ضلعين متناظرين في مضلعين متشابهين هي 4) إذا كانت أطوال الأضلاع المتناظرة في مثلثين متناسبة، فإن المثلثين ؟ متشابهان وفق . 5) أحيانًا يطلق على معامل التشابه بين مضلعين اسم - 6 إذا كانت A = F ، وكان AC وفق . ، فإن ABAC - AEFD BA AC EF FD 48 الفصل 6 التشابه وزارة التعليم Ministry of Education 2024-1446

مراجعة الدروس 6-1 المضلعات المتشابهة (ص 12-19 1) حدد ما إذا كان المضلعان أدناه متشابهين أم لا، وإذا كانا كذلك، مثال 1 فاكتب عبارة التشابه ومعامل التشابه، ووضح إجابتك. حدد ما إذا كان المضلعان أدناه متشابهين أم لا. برر إجابتك. وإذا كانا كذلك، فاكتب عبارة التشابه ومعامل التشابه، ووضح إجابتك. 6 M6 F 16 G B 6 C 12 K T6 U ھے 62 4 10 W 10 A 16 A 6 D 14 24 24 E 16 H V L (2) المثلثان في الشكل أدناه متشابهان أوجد قيمة x . V B 16 12 C H G x 22 M (3) النظام الشمسي في نموذج دقيق لنظامنا الشمسي، وضعت سميرة الأرض على بعد 1ft من الشمس، علما بأن المسافة الحقيقية بين الأرض والشمس mi 93000000، إذا كانت المسافة من بلوتو إلى الشمس mi 3695950000، فعلى أي بعد من الشمس ستضع سميرة بلوتو في نموذجها ؟ الخطوة 1 : حدد الزوايا المتناظرة المتطابقة JET, KUL ME W الخطوة 1 : اختبر النسب بين أطوال الأضلاع المتناظرة. 1 6 JK 2 12 KL 24 = TU " UV LM 12 JM = = VW 14 TW 6 بما أن الأضلاع المتناظرة غير متناسبة، فإن المضلعين TUVW, JKLM غير متشابهين المثلثات المتشابهة (ص 20-28 6-2 حدد ما إذا كان المثلثان في كل من السؤالين الآتيين متشابهين أم لا، وإذا كانا كذلك، فاكتب عبارة التشابه، ووضح إجابتك. I (5 4 5 A (4 5 7 B H 6 E 13 6 9 7.5 D مثال 2 حدد ما إذا كان المثلثان الآتيان متشابهين أم لا، وإذا كانا كذلك، فاكتب عبارة التشابه، ووضح إجابتك. Y 12 X 9 Z W 16 CWZX = XZY لأنهما زاويتان ،قائمتان، والآن اختبر تناسب طولي ساقي المثلثين القائمين. F G C 6 أشجار يريد عبد الله أن يقدّر ارتفاع شجرة، فوقف على WZ XZ 3 9 XZ = = 4 12 مسافة ft منها، فكانت نهاية ظله ونهاية ظل الشجرة عند وبما أنه يوجد ضلعان في المثلث الأول، طولاهما متناسبان مع النقطة نفسها، إذا كان طول عبد الله 6ft و 4in وطول ظله طولي نظيريهما في الثاني، وأن الزاويتين المحصورتين بينهما ft 15، فما ارتفاع الشجرة؟ متطابقتان، فإنّ AWZX - XZY ، وفق نظرية التشابه SAS. الفصل 6 دليل الدراسة والمراجعة 49 Ministry of Education 2024-1446

H 2y-5 y+12 F 3x+7 K 4x-1 G وزارة التعليم Ministry of Education 2024-1446 دليل الدراسة والمراجعة الفصـ 6 6-3 المستقيمات المتوازية والأجزاء المتناسبة ( ص 30-38) أوجد قيمة x في كلُّ من السؤالين الآتيين: مثال 3 جبر: أوجد قيمة كل من x, y . FK = KG تعريف التطابق 1 - 3x + 7 = 4x بالتعويض (8 10 8 x 18 4 x (7 5 12 و شوارع أوجد المسافة على امتداد شارع المطار بين الشارعين 37 36 ، بفرض أن الشوارع 38 37 36 متوازية شارع 38 240 ft. 300 ft شارع 37 شارع 36 شارع المطار شارع 7 -x = -8 x = 8 FJ = JH بالطرح بقسمة كلا الطرفين على (1) تعريف التطابق 5 - y + 12 = 2y بالتعويض بالطرح -y=-17 y = 17 200 ft بقسمة كلا الطرفين على (1) Y 14 28 W x Z X 12 6-4 عناصر المثلثات المتشابهة (ص 39-47) أوجد قيمة المتغير في كلّ من السؤالين الآتيين مقربا إجابتك إلى مثال 4 أقرب جزء من عشرة أوجد قيمة x . استعمل نظرية منصف زاوية في مثلث لكتابة تناسب. نظرية منصف زاوية في مثلث. WX YW (11 (10) 10 36 8 9 W 10 13.5 12 عين الإنسان: تستعمل عين الإنسان المثلثات المتشابهة لقلب الشيء وتصغيره عندما . يمر خلال العدسة إلى الشبكية فما المسافة بين عدسة العين والشبكية؟ الشبكية 0.25 in xin العدسة x 12 28-x 14 بالتعويض 14 x(12) = x) - (28) خاصية الضرب التبادلي 336 - 12x = 14x 336 = 26x 32 ft 8ft 12.9 ~ x بالتبسيط بإضافة 12x لكلا الطرفين بقسمة كلا الطرفين على 26 الفصل 6 التشابه 50

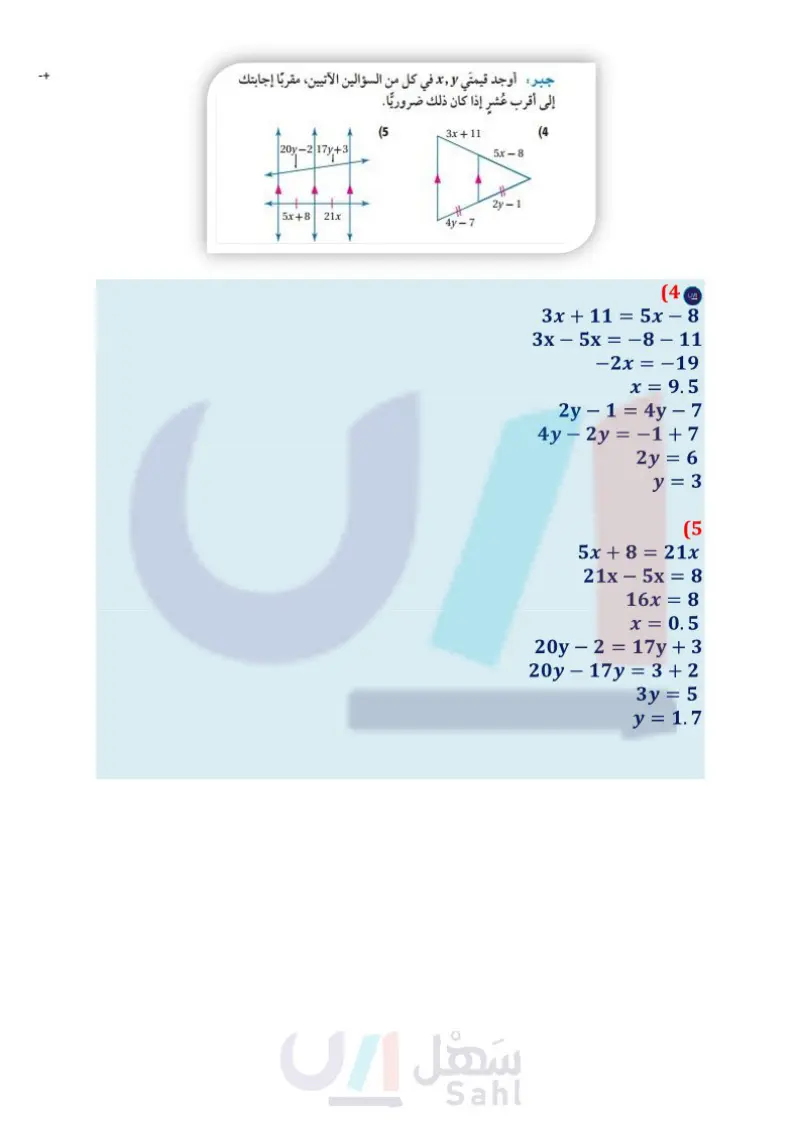
اختبار الفصل 6 حدد ما إذا كان المضلعان متشابهين أم لا في كل من السؤالين الآتيين، (6) جبر وإذا كانا كذلك، فاكتب عبارة التشابه ومعامل التشابه، وضح إجابتك. (1 A X 14 Y 7 26 B 24.5 C 21 R (2 L 10 F 9 AMNP متطابق الأضلاع، محيطه 18 + 12 ، إذا كانت QR قطعة منصفة فيه، فما قيمة QR؟ جبر: AABC قائم الزاوية ومتطابق الضلعين، وطول وتره ، إذا كانت DE قطعة منصفة للوتر وأحد ضلعي القائمة فيه وطولها 4x ، فما محيط AABC؟ (8) نماذج لدى سالم نموذج لسيارة سباق حقيقية، إذا كان طول السيارة الحقيقية ft و in 6 ، وطول النموذج in 7 ، فما معامل تشابه النموذج إلى السيارة الحقيقية؟ أوجد قيمة x في كل من السؤالين الآتيين: 21 A A 26 30 A 251 x 40 (10 جبر أوجد كل طول مشار إليه في كل من السؤالين الآتيين: الفصل 6 اختبار الفصل الت51 Ministry of Education 2024-1446 W WZ, UZ (11 x+7 12 20 Z +1 U Y K 10.4 M 13 12 L 8 P 10 G4 HT S (3) أبراج: استعمل المعلومات الآتية لحل السؤالين الآتيين: لتقدير ارتفاع برج Jin Mao في شنغهاي في الصين، شاهد سائح قمة البرج في مرأة موضوعة على الأرض ووجهها إلى أعلى. 1.92m B 0.4m C 87.6m E xm جبر (a ) كم مترا ارتفاع البرج تقريبا؟ لماذا تكون طريقة الانعكاس في المرآة في هذه الحالة أفضل للقياس غير المباشر لارتفاع البرج من استعمال الظل ؟ أوجد قيمتي x, y في كل من السؤالين الآتيين، مقربا إجابتك إلى أقرب عشر إذا كان ذلك ضروريا. (5 3x + 11 KL (12) 20y-217y+3 5x 8 2y-1 5x+8 21x 4y-7 (4)

القصد 6 الإعداد للاختبارات تعيين اللامثال أحيانًا تتطلب أسئلة الاختيار من متعدد تحديد أي البدائل المعطاة تعد لا مثالًا صحيحًا، وتتطلب هذه الأسئلة أسلونا مختلفا لحلها. استراتيجيات تعيين اللامثال 52 الخطوة | اقرأ المسألة وافهمها. . اللامثال: اللامثال هو بديل من بدائل الإجابة لا يحقق شروط المسألة. . كلمات أساسية: ابحث عن كلمة لا، أو أي كلمة تدلّ على النفي (تكتب عادة بخط غامق أو يوضع تحتها خط لتفهم منها أن المطلوب منك أن تجد لا مثالاً. | الخطوة 2 اتبع الإرشادات والخطوات الآتية؛ لمساعدتك على تعيين اللامثال: عين بدائل الإجابة الواضح عدم صحتها واحذفها. . احذف البدائل التي تبدو بعيدة عن محتوى السؤال. . احذف البدائل ذات الوحدات غير الصحيحة. اختبر بدائل الإجابة المتبقية. امثال اقرأ المسألة جيدا، حدد المطلوب فيها، ثم استعمل المعطيات لحلها. أي مما يأتي لا يكفي لإثبات أن: AQMN ~ AQRS ZQMN=ZQRS A MN || RS B QN = NS C QM QN D QR QS الفصل 6 التشابه S M N R وزارة التعليم Ministry of Education 2024-1446

الحرف "لا" المكتوب بالخط الغامق، يُشير إلى أنه يتعين عليك أن تجد لا مثالا، اختبر كلا من بدائل بدائل الإجابة باستعمال مبادئ تشابه المثلثات لترى ما إذا كان أي منها لا يثبت أن AQMN ~ AQRS. البديل LQMN = LQRS A إذا كانت QMN = QRS ، فإن AQMN - AQRS وفق مسلمة التشابه AA . البديل : MN || RS إذا كان MN || RS ، فإن QMN = LQRS ؛ لأنهما زاويتان متناظرتان بالنسبة لمستقيمين متوازيين قطعهما القاطع QR ، لذلك QMN - AQRS وفق مسلمة التشابه AA. البديل QN = NS C إذا كانت QN = NS ، فإننا لا نستطيع أن نستنتج أن AQMN - AQRS ؛ لأننا لا نعرف أي شئ عن QM, MR ، لذلك فالبديل C يُعد لامثالًا، والإجابة الصحيحة هي .C. وإذا كان لديك وقت فاختبر البديل D للتأكد من أنه مثال صحيح. تمارين ومسائل اقرأ كل سؤال مما يأتي، ثم اكتب رمز الإجابة الصحيحة: أي مما يأتي لا يكفي لإثبات أن AGK - AMG؟ (1) أي التناسبات التالية غير صحيحة في الشكل أدناه ؟ G H I K AD CD A CD DB AB AC B AC AD AB ZGKI ZHGI A C B DB CD D B GI IK AB AC أي شكل يمكن أن يكون مثالاً مضافا للتخمين أدناه ؟ إذا كانت جميع زوايا شكل رباعي قوائم فإنه مربع متوازي الأضلاع المستطيل المعين D شبه المنحرف C GI IK ZIGK ZIHG D (4) أي مثلثين مما يأتي ليسا بالضرورة متشابهين؟ مثلثان قائما الزاوية في كل منهما زاوية قياسها °30 مثلثان قائما الزاوية في كل منهما زاوية قياسها °45 مثلثان متطابقا الساقين مثلثان متطابقا الأضلاع الفصل 6 الإعداد للاختبارات 53 Ministry of Education 2024-1446

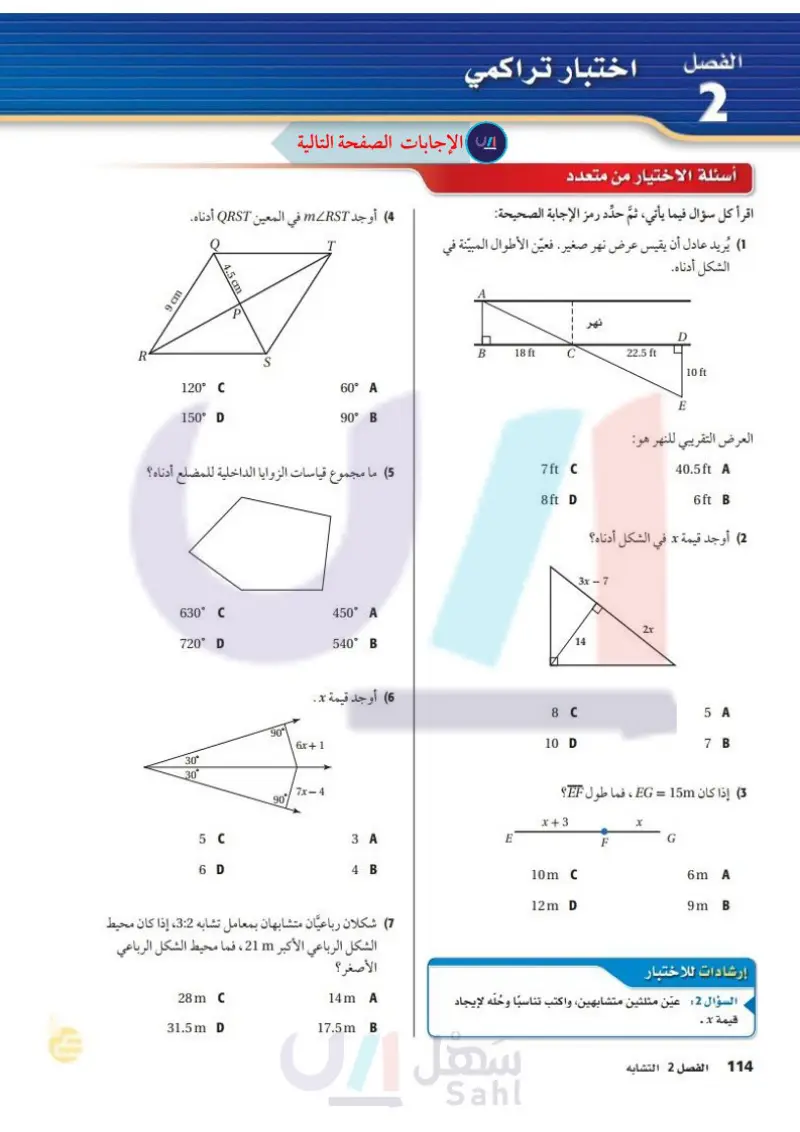
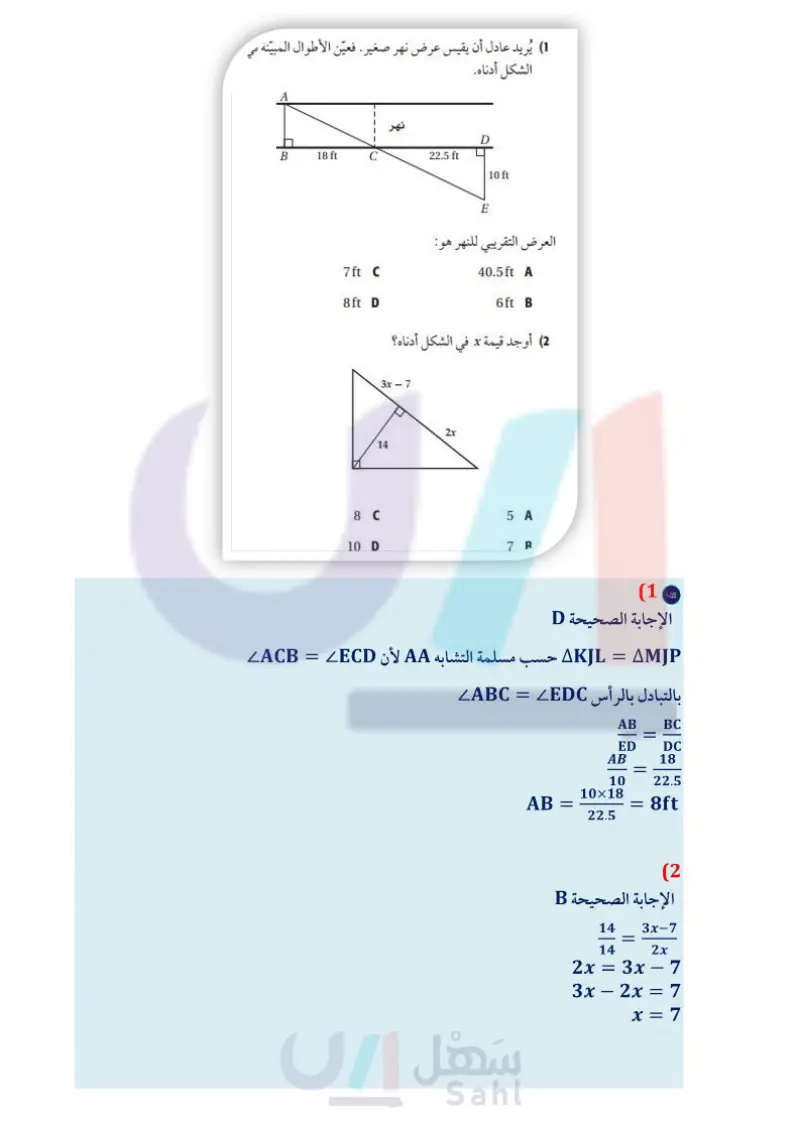
وزارة التعليم Ministry of Education 2024-1446 9 cm 4) أوجد mRST في المعين QRST أدناه. R 120° C S 150° D اختبار تراكمي 6 أسئلة الاختيار من متعدد اقرأ كل سؤال فيما يأتي، ثم حدد رمز الإجابة الصحيحة: (1) يُريد عادل أن يقيس عرض نهر صغير. فعين الأطوال المبينة في الشكل أدناه. B 18 ft 22.5 ft 10 ft 60° A E 90° B (5) ما مجموع قياسات الزوايا الداخلية للمضلع أدناه؟ 7ft C 8ft D العرض التقريبي للنهر هو 40.5ft A 6ft B (2) أوجد قيمة x في الشكل أدناه؟ 630°C 720° D 450° A 540 B 3x 7 14 2x (6) أوجد قيمة x . 30° 30° 90 6x + 1 5 C 6 D 7x-4 90 10 D 5 A 7 B (3) إذا كان EG = 15m ، فما طول EF؟ x+3 x 3 A E G F 4 B 10m C 6m A 12m D 9m B (7) شكلان رباعیان متشابهان بمعامل تشابه 3:2، إذا كان محيط الشكل الرباعي الأكبر m 21 ، فما محيط الشكل الرباعي الأصغر؟ 28m C 14m A 31.5m D 17.5m B إرشادات للاختبار السؤال 2 عين مثلثين متشابهين واكتب تناسبا وحله لإيجاد قيمة x . الفصل 6 التشابه 54

أسئلة ذات إجابات قصيرة اكتب إجابتك في ورقة الإجابة. 8) هندسة إحداثية مثل في المستوى الإحداثي الشكل الرباعي ABCD الذي رؤوسه (1) (6)B8, 2, C ,(33) وحدد ما إذا كان متوازي أضلاع أم لا. (9) إذا كان MN || BC في المثلث أدناه، فأوجد قيمة x . 12) إذا كان RS تنصف VRU في المثلث أدناه، فأوجد قيمة x . 16 R 11.2 V 7 S U x (13) يبين مقياس رسم خريطة أن cm = 25km 1، ما المسافة الحقيقية بين مدينتين، إذا كانت المسافة بينهما على الخريطة 4.5cm (14) ما قيمة x في الشكل أدناه ؟ 62° (5x+2) A 4x-6 M 24 B 3x-2 N 20 C (10) الشكل الرباعي WXYZ معين، إذا كان 110 = mZXYZ، فأوجد mZZWY . أسئلة ذات إجابات مطولة اكتب إجابتك في ورقة الإجابة مبينا خطوات الحل. (15) استعمل الشكل أدناه للإجابة عن كل من الأسئلة الآتية: X 2 R Y إذا كان QR || XY ، فما العلاقة بين الأطوال RZ, YR, QZ, XQ ؟ إذا كان 20 = QR || XY, XQ = 15, Q2 = 12, YR ، فما طول RZ ؟ QR || XY, XQ = QZ, QR = 9.5:15 15! (c فما طول XY؟ Z W. X (11) ما المعاكس الإيجابي للعبارة أدناه ؟ إذا كان صالح مولودًا في الرياض، فإنه مولود في السعودية. 15 14 13 12 11 8 10 9 7 6 5 4 3 2 1 6-3 مهارة سابقة 6-1 6-4 مهارة | مهارة سابقة سابقة 6-3 مهارة سابقة 6-1 مهارة مهارة مهارة مهارة سابقة سابقة سابقة سابقة 6-2 6-2 الفصل 6 اختبار تراكمي ال 55م Ministry of Education 2024-1446 هل تحتاج إلى مساعدة إضافية؟ إذا لم تستطع الإجابة عن السؤال.. فعد إلى الدرس..