حل المعادلات والمتباينات النسبية - رياضيات2-2 - ثاني ثانوي

5-6 فيما سبق: حل المعادلات والمتباينات النسبية Solving Rational Equations and Inequalities درست تبسيط عبارات نسبية. الدرس (1-5) والان لماذا؟ يبلغ رسم العضوية في أحد الأندية الرياضية 200 ريال شهريا بالإضافة إلى 10 ريالات عند كل زيارة للنادي. فإذا كان أحد أحل معادلات نسبية. الأعضاء يزور النادي x مرة شهريا، فإنه سيدفع مبلغا مقداره أحل متباينات نسبية. (2010) ريالا في الشهر. ويمكن حساب التكلفة الفعلية المفردات: لكل زيارة للعضو باستعمال العبارة : المعادلة النسبية rational equation المتباينة النسبية rational inequality www.ien.edu.sa 200+10 x X ، حيث x عدد مرات زيارة النادي. 200+10 x ولحساب عدد مرات زيارة أحد الأعضاء للنادي إذا كانت التكلفة الفعلية للزيارة الواحدة 30 ريالا، عليك أن تحل المعادلة 30 = مراجعة المفردات الحل الدخيل هو الحل الذي لا يحقق حل المعادلات والمتباينات النسبية: تُسمى المعادلة التي تحتوي على عبارة نسبية أو أكثر معادلة نسبية، ويكون حل هذه المعادلة عادة أسهل عندما تتخلص من المقامات، وذلك بضرب طرفي المعادلة في LCM لها. ومن الممكن الحصول على حلول دخيلة عند ضرب طرفي المعادلة النسبية في LCM للمقامات؛ لذا فإنه من الضروري التحقق من صحة الحل لاستثناء القيم التي تجعل أحد مقامات المعادلة صفرا. مثال 1 حل معادلة نسبية 3 حل المعادلة 773 2 - x - 10 x 2 + x + 15 = 2x *x+5 المعادلة الأصلية. LCM للمقامات هو (5) + x + x . 2x x+5 x2 - x - 10 x2 + x + 15 3 x + 3 (x+3)(x+5)(2x) (x+3)(x+5)(x²-x-10) (x+3)(x + 5)3 x + 3 x +5 x2 + x + 15 (x+3)(x+5)(2x) *+5 1 (x+3)(x+5)(x² - x - 10) (x+3)(x+5)3 +3 1 x2 + 8x + 15 1 (x+3)(2x) (x²-x-10)=3(x+5) 2x2 + 6x - x2 + x + 10 = 3x + 15 x2 + 7x + 10 = 3x + 15 x2 + 4x - 5 = 0 (x+5)(x-1)=0 0 = 5 + x أو 0 = 1 - x 5- = x أو x = 1 المعادلة الأصلية اضرب المعادلة في LCM للمقامات اختصر العوامل المشتركة بسط خاصية التوزيع بسط اطرح 15 + 3x من كلا الطرفين حلل إلى عوامل خاصية الضرب الصفري وزارة التعليم الدرس - حل المعادلات والمتباينات النسبية 105 2024-1446

تحقق اختبر 5- = x : اختبر 1 = x 2x 22 - 2 - 10 المعادلة الأصلية = x+5 x 2 + x + 15 x+3 x=-5 2(-5) (-5)2-(-5)-10 ? 3 -5+5 (-5)²+8(-5)+15 -5+3 بسط 25+5 10 -10 X 0 25-40+15 +- 1/3 2x 22 - x - 10 المعادلة الأصلية = : x+5 x2 + 8x + 15 x +3 2(1) x=1 12-1-10 1 1+5 1²+8(1) +15 1+3 -10 بسط 6 24 8 10 ? وحد المقامات + 24 بسط إذا نتج عن تعويض أحد الحلول صفر في أحد مقامات المعادلة، وجب استثناء هذا الحل. وبما أن 5 = x ينتج عن تعويضها في المعادلة صفر في المقام فإنها تُستثنى من الحلول لذا يكون الحل هو 1 = x . تحقق من فهمك 5 +2= y-2 (1 (1 3n " 211 + 2 2p + 1 p - 2 = p2 + 2p - 8 + 2 P+4 (10) 7n 3n+3 5 4n-4 = إرشادات للدراسة مسائل المسافة عندما تتضمن مسائل المسافة الذهاب والعودة، فإن المسافة في الذهاب تساوي المسافة في العودة ما لم يذكر خلاف ذلك. يمكنك استعمال المعادلة التي تربط بين المسافة d والسرعة " والزمن الحل كثير من المعادلات النسبية. وأكثر الأشكال شيوعا لهذه المعادلة هو d = rt . وكذلك يمكنك استعمال الشكلين الآخرين، وهما: t= مثال 2 من واقع الحياة | استعمال المعادلات النسبية في مسائل الحركة تجديف ركب سعيد قاربًا سرعته 6mi/h في المياه الراكدة وسار به دون توقف مسافة 10mi؛ نصفها في اتجاه التيار ونصفها الآخر عكسه فاستغرق زمناً قدره 3 أوجد سرعة التيار. افهم معطيات المسألة هي: سرعة القارب في المياه الراكدة، وكذلك المسافة التي قطعها ذهابًا وإيابًا والزمن المستغرق في قطع المسافة كاملة. والمطلوب إيجاد سرعة التيار (0). خطط : المسافة التي قطعها سعيد هي mi 5 في اتجاه التيار، و mi 5 عكس اتجاه التيار. والمعادلة التي تُستعمل للحل هي : d = rt أو = t ، حيث r السرعة، d المسافة، الزمن الكلى الزمن مع الزمن عكس اتجاه التيار اتجاه التيار 3h 6-0 6+0 106 الفصل 5 العلاقات والدوال النسبية الزمن. وزارة التعليم Ministry of Education 2024-1446

اكتب المعادلة . (0) - 6) (0 +6 اضرب كل من الطرفين في LCM للمقامات (2) - 6) + 6) (0) - (6) (60) اختصر العوامل المشتركة بسط خاصية التوزيع بسط اطرح 60 من كلا الطرفين حلل إلى عوامل اقسم كل من الطرفين على 3 خاصية الضرب الصفري المعادلة الأصلية 0 = 4 بسط بسط ووحد المقامات 1 v=4 5 5 =3 6+ 2 6-v 5 +(6+v)(6v) 6 + 20 = (6+ v)(6v)(3) 6-v +(6+v)(6-v). 5 == (6+ v)(6v)(3) 6+0 1 1 6-v 1 (6v)(5) + (6+v)(5) = (36 v2)(3) 30-50+30+ 5v = 108-3v2 60 = 108 - 3v² 0=-3v²+48 0=-3(v+4)(v - 4) 0(v4)(v4) (مرفوض؛ لأن السرعة لا يمكن أن تكون سالبة) 4- = 7 حل 5 + تحقق 3 = 6 + 2 6-v 5 5 + 3 6+4 6-4 ✓ 1+53 الربط بالحياة تمثل المخلفات البلاستيكية لذا؛ فإن سرعة التيار هي 4mi/h . تحقق من فهمك (2) طيران إذا قطعت طائرة مسافة 2368mi في رحلة ذهاب وعودة دون توقف في 7h، وكانت سرعة الريح 20mih ، فما سرعة الطائرة في الريح الساكنة؟ خطورة عالية وكارثة بيئية يمكنك حل المسائل الحياتية التي تتعلق بالأعمال عادة باستعمال معادلات نسبية. وصحية على الإنسان والحياة البرية والبحرية لما بها مثال 3 من واقع الحياة استعمال المعادلات والمتباينات النسبية في مسائل العمل من مواد كيميائية لا تتحلل خدمة المجتمع يقوم طلاب الصفين الأول الثانوي والثاني الثانوي في أحد الأحياء بحملة توعية بخطر في التربة وتشمل العلب البلاستيكية والأطعمة والمنظفات والمشروبات الغازية وغيرها. وتستهلك الدول العربية منها 50 مليار علبة سنويا. إرشادات للدراسة جداول تكوين الجداول - كما في المثال 3 - يفيد في تنظيم وحل المسائل بشكل عام. النفايات البلاستيكية لسكان الحي . فإذا علمت أن هذا العمل يحتاج إلى 24 ساعة إذا قام به طلاب الصف الثاني الثانوي، و18 ساعة عمل إذا قام به طلاب الصفين معًا، فكم ساعةً يحتاج طلاب الصف الأول الثانوي للقيام بالعمل وحدهم؟ افهم المعطيات هي: الزمن الذي يحتاج إليه طلاب الصف الثاني الثانوي لإتمام العمل، والزمن الذي يحتاج إليه طلاب الصفين معًا لإتمام العمل والمطلوب إيجاد الزمن الذي يحتاج إليه طلاب الصف الأول الثانوي لإتمام العمل خطط يستطيع طلاب الصف الثاني الثانوي إتمام العمل في .24h. وعليه فإن معدل عملهم يساوي من العمل في الساعة الواحدة. في حين يبلغ معدل عمل طلاب الصف j الأول الثانوي - من العمل في الساعة الواحدة، أما معدل عمل طلاب الصفين معا فهو من العمل في الساعة الواحدة. معدل عمل معدل عمل طلاب الصف طلاب الصف الأول الثانوي الثاني الثانوي معدل عمل طلاب الصفين معا 1 j وزارة التعليم الدرس 6- حل المعادلات والمتباينات النسبية 1070 2024-1446

حل تحقق 1 1 24 اكتب المعادلة 72j = 1 2 + 72 اضرب كل من الطرفين في LCM للمقامات وهو (72 3 72 اختصر العوامل المشتركة + 721 = 72j بسط اطرح 3 من كلا الطرفين 3j+72 = 4j 72 = j 1 1 1 المعادلة الأصلية + = 24 18 j j=72 ? 1 + 18 LCM للمقامات هو 72 3 1 ? 4 + 72 72 بسط ✓ إرشادات للدراسة يحتاج طلاب الصف الأول الثانوي إلى 72 لإتمام العمل وحدهم. تحقق من فهمك (3) طلاء يحتاج ناصر ومحمد إلى 6 لطلاء سور إذا عملا معًا، ويحتاج ناصر إلى 10h للقيام بالعمل وحده. فكم ساعة يحتاج محمد إذا قام بالعمل وحده؟ حل المتباينات النسبية المتباينات النسبية ، هي المتباينات التي تحتوي على عبارة نسبية أو أكثر. ولحلها اتبع الخطوات الآتية: مفهوم أساسي حل المتباينات النسبية الخطوة 1: حدد القيم المستثناة وهي القيم التي يكون عندها المقام صفرا الخطوة 2 حل المعادلة المرتبطة والتي تحصل عليها بوضع رمز المساواة بدلا من رمز التباين في المتباينة أضف مطويتك الخطوة 3: استعمل القيم التي حصلت عليها في الخطوتين السابقتين ؛ لتقسيم خط الأعداد إلى فترات الخطوة 4 اختبر قيمة من كل فترة لتحديد الفترات التي تحقق أعدادها المتباينة مثال 4 حل متباينة نسبية x+1 تقسيم خط الأعداد حل المتباينة النسبية 41 - من الضروري استعمال القيم المستثناة وحلول المعادلة المرتبطة جميعها عند تقسيم خط الأعداد إلى فترات الخطوة :1 القيمة المستثناة في هذه المتباينة هي 2. الخطوة 2 : حل المعادلة المرتبطة: x+1 4 x-2 3 1 x-2 1 = 12(x-2)+1 1 4 المعادلة المرتبطة 2 - 2123 - 2 - 12 اضرب في LCM للمقامات : (2 – x)12 1 4x2 - 8 - 12 = 3x2 - 3x - 6 1 خاصية التوزيع 108 الفصل 5 العلاقات والدوال النسبية x2 - 5x - 6 = 0 (x6)(x+1)= 0 1- = x أو 6 = x اطرح 6 - 3 - 3x2 من كلا الطرفين حلل إلى عوامل خاصية الضرب الصفري وزارة التعليم Ministry of Education 2024-1446

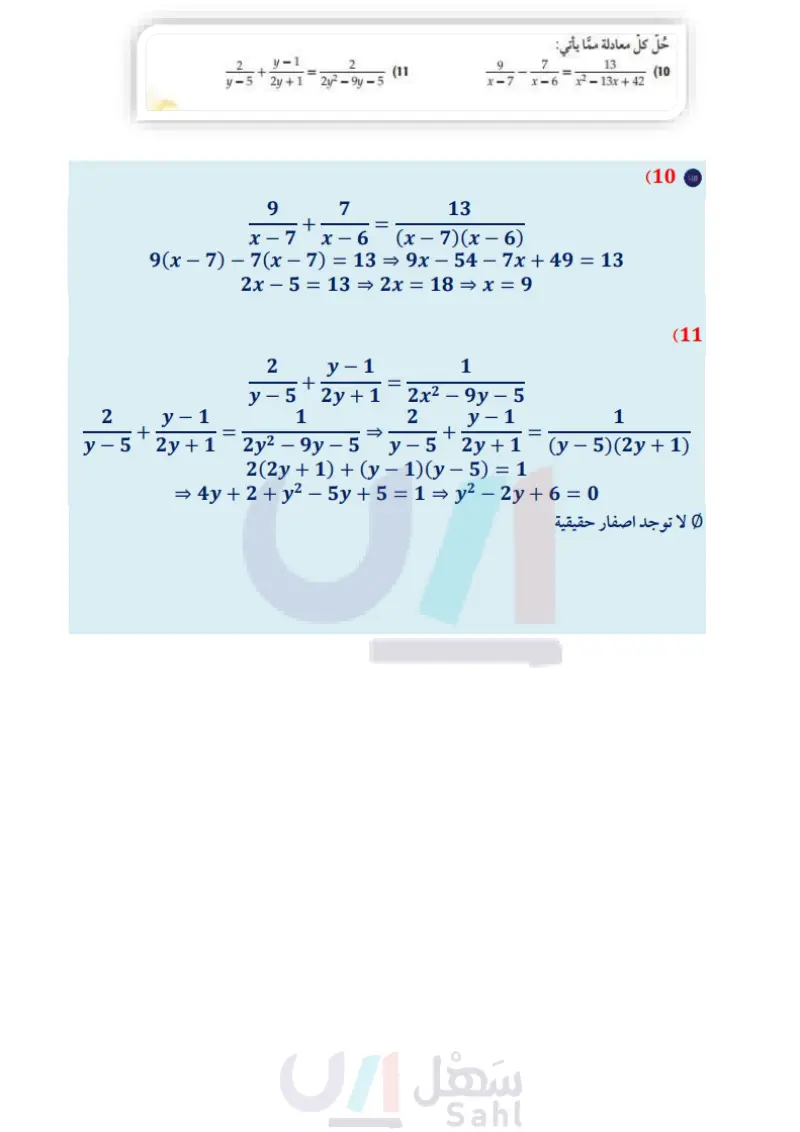
الخطوة 3: ارسم . خطا رأسيًا عند القيمة المستثناة، وعند حلّي المعادلة وذلك لتقسيم خط الأعداد إلى فترات. 22 اختبر 8 = x 8 8 7 6 5 4 3 2 1 0 -1 -2 الخطوة 4 اختبر قيمة من كل فترة لتحديد ما إذا كانت الأعداد في الفترة تحقق المتباينة. اختبر 4 = x اختبر 0 = x اختبر 3 = x 4+1 0 0+1 4-2 4 4 0-2 0+ -1 + 4 شما -3+1 4 الجملة صحيحة عندما 4 = x = 3 x ؛ لذا فإن الحل هو -1 > x أو 6 > x > 2 . تحقق من فهمك 3.x 5x مثال 1 حُلَّ كلَّ معادلة مما يأتي: 1-135-193 (2 (1 5 3 12 8 9 5 = (4) (3 x+2 x-2 x2 4 -5 -4 x2 - 9x + 20 مثال 2 5) مسافة قطع وليد مسافة km 40 ذهابًا وعودة مستعملًا دراجته التي سرعتها km/h 11.5 عندما تكون الريح ساكنة، فإذا سار في اتجاه الريح زمناً قدره ساعة و 20 دقيقة، وساعتان ونصف الساعة عكس اتجاه الريح. اكتب عبارة تمثل الزمن الذي استغرقه أثناء سيره في اتجاه الريح. ) اكتب عبارة تمثل الزمن الذي استغرقه أثناء سيره عكس اتجاه الريح. اكتب معادلة نسبية وحلها لإيجاد سرعة الريح. مثال 3 (6) تبليط يعمل كل من أحمد وعلي في التبليط، إذا كان أحمد يحتاج إلى 6 أيام لتبليط فناء منزل وحده، في حين يحتاج علي إلى 5 أيام للقيام بالعمل نفسه. فكم يوما يحتاجان إليه إذا عملا معا في تبليط هذا الفناء؟ مثال 4 حُلَّ كلَّ متباينة مما يأتي: 3 (9 + 4 x - 3 x +4 3-> (7 تأكد تدرب وحل المسائل مثال 1 حُلَّ كل معادلة مما يأتي: 2 y-1 y-5 2y+1 2 9 7 (11 = 2y2-9y-5 x-7 x-6 وزارة التعليم الدرس - حل المعادلات والمتباينات النسبية 109 2024-1446 13 x2 - 13x + 42 (10

المثالان 23 (12) بناء : تحتاج مجموعة من العمال إلى 12 يوما لبناء مرآب سيارات، في حين تحتاج مجموعة أخرى إلى 16 يوما لإنجاز العمل نفسه، فكم تحتاج المجموعتان معا لبناء المرآب نفسه؟ (13) طيران سارت طائرة مسافة معينة في عكس اتجاه الريح في 20 ، واحتاجت إلى 16h لقطع المسافة نفسها في رحلة العودة، ولكن في اتجاه الريح. إذا كانت سرعة الطائرة في أثناء الريح الساكنة mi/h 500 ، فما سرعة الريح خلال الرحلة؟ مثال 4 (14) حل المتباينة: 13 3 + 5x 6x 15) تمثيلات متعددة : افترض أن = = 1 + 23 x-3 جبريًا حُلّ هذه المعادلة، وهل يوجد حل دخيل؟ (6) بيانيا : مثل: = = 2 1 + 23 = لا بيانيا على المستوى الإحداثي نفسه، حيث 5 > x > 0 . تحليليا : ما قيمة (قيم ) x التي يتقاطع عندها التمثيلان البيانيان؟ وهل يتقاطعان عند الحل الدخيل للمعادلة الأصلية؟ d) لفظيا : استعمل المعلومات التي حصلت عليها في الفرع (c) ؛ لتصف كيف يمكنك استعمال التمثيل البياني للمعادلة لتحديد ما إذا كان أحد الحلول حلا دخيلًا. (16) حل المعادلة. 3 = 2y-2 4-y y²-y-12 2 y+3 ، وتحقق من صحة حلك. مسائل مهارات التفكير العليا 17) مسألة مفتوحة : أعط مثالا على معادلة نسبية يمكن حلها بضرب طرفي المعادلة في (4 – x + 3)(x)4 . 18 تحد: حل المعادلة : x+4 -5 20 = 25 1 (19) تبرير وضّح لماذا يجب التحقق من حلول المعادلة النسبية. 20 اكتب عند استعمال تطبيق القوائم وجداول البيانات في الحاسبة البيانية لاستكشاف الدالة: = (f(x ، فإن الحاسبة البيانية تعطي خطأ عند القيمتين 2 = x و 3 = x . وضّح ماذا يعني ذلك؟ 1 x²-x-6 11 10 ؟ (22) ما قيمة x في المعادلة 4 =| a+2 a+5 36 a²+7a+10 تدريب على اختبار (21) ما حل المعادلة: 1 -7 A 1 D C B -1 A 2 مراجعة تراكمية 23) حدد إذا كانت العلاقة المجاورة تمثل تغيرا طرديًا، أم تغيرًا عكسيًّا، أم غير ذلك: (الدرس 5-5) (24) مثل الدالة . x +4 x2 + x + 12 = (f(x بيانيا (الدرس 4-5) 25) اكتب الحدود الثلاثة التالية في المتتابعة ... (مهارة سابقة) 110 الفصل 5 العلاقات والدوال النسبية (+) (*1) 7D x 14 28 56 112 y 3 1.5 0.75 0.375 وزارة التعليم Ministry of Education 2024-1446