المتتابعات والمتسلسلات الحسابية - رياضيات2-2 - ثاني ثانوي
الفصل الرابع: العلاقات والدوال العكسية والجذرية
الفصل الخامس: العلاقات والدوال النسبية
الفصل السادس: المتتابعات والمتسلسلات
نشاط الفصل الرابع: العلاقات والدوال العكسية والجذرية
نشاط الفصل الخامس: العلاقات والدوال النسبية
المتتابعات والمتسلسلات الحسابية Arithmetic Sequences and Series 6-2 فيما سبق درست تمييز المتتابعة الما ذار؟ في القرن الثامن عشر، طلب معلم للرياضيات من طلابه في المرحلة الابتدائية أن يجدوا مجموع الأعداد الصحيحة من 1 إلى 100 فقام أحد الطلاب واسمه كارل الحسابية الدرس (1-6) جاوس (Karl Gauss) بإعطاء الإجابة الصحيحة خلال ثوان، مما أثار استغراب المعلم. وقد أصبح هذا الطالب كارل جاوس" أحد أفضل علماء الرياضيات والان أجد حدود متتابعة على مر العصور. حسابية وحدها النوني لقد حلَّ جاوس هذا السؤال باستعمال المتسلسلات الحسابية. أجد أوساطا حسابية. . أجد مجموع حدود متسلسلة حسابية منتهية. المفردات: الأوساط الحسابية arithmetic means المتتابعات الحسابية: لقد استعملت صيغة النقطة والميل في الدرس 1 - 6؛ www.icn.edu.sa لإيجاد قيمة حد معين في متتابعة حسابية. ويمكنك إيجاد معادلة تستطيع من خلالها إيجاد أي حد من حدود متتابعة حسابية باستعمال الأسلوب نفسه. ففي المتتابعة الحسابية a ..... (y-y₁) =m(x-x₁) 43 42 41 التي أساسها d يكون: صيغة الميل والنقطة المتسلسلة series المتسلسلة الحسابية arithmetic series (x, y) = (n, a,), (x₁, y₁) = (1, a₁), m = d (aa) d(n - 1) aa+d(n-1) اجمع 4 للطرفين ويمكنك استعمال هذه الصيغة لإيجاد قيمة أي حد من حدود المتتابعة الحسابية، وذلك بمعرفة الحد الأول والأساس. المجموع الجزئي partial sum رمز المجموع sigma notation 130 مفهوم أساسي الحد النوني في المتتابعة الحسابية تستعمل الصيغة الآتية للتعبير عن الحد النوني في متتابعة حسابية حدها الأول 4 ، وأساسها ، حيث 11 عدد طبيعي. aa+(n-1) d ستشتق هذه الصيغة في السؤال (58) مثال 1 إيجاد حد معين في متتابعة حسابية أوجد قيمة الحد الثاني عشر في المتتابعة الحسابية. 9, 16, 23, 30, ... الخطوة 1: أوجد أساس المتتابعة. الفرق بين أي حدين متتاليين: 7 = 9 - 16 إذن 7 = d الخطوة 2: أوجد قيمة الحد الثاني عشر. aa₁+ (n-1)d a129(121)(7) تحقق من فهمك = 9+ 77 = 86 الحد النوني في المتتابعة الحسابية a₁=9, d=7, n=12 بسط أضف إلى مطويتك أوجد قيمة الحد المطلوب في كلُّ من المتتابعتين الحسابيتين الآتيتين: 1) علما بأن : 9 = d = 6, n ,4- = 4 (1) 20 علما بأن : 8- = d ,15 = 41 وزارة التعليم الفصل 6 المتتابعات والمتسلسلات Ministry of Education 2024-1446

إرشادات للدراسة التحقق من صحة الحل تحقق من صحة الحل باستعمال صيغة الحد النوني التي أوجدتها لحساب الحدود الثلاثة الأولى في المتتابعة تنبيه أساس المتتابعة الحسابية لا تخطئ في تحديد إشارة أساس المتتابعة الحسابية | وتحقق دائما من أن صيغة الحد النوني تعطي حدود المتتابعة جميعها. إذا أعطيت مجموعة من الحدود في متتابعة حسابية، فإنه يمكنك كتابة صيغة للحد النوني في هذه المتتابعة. مثال 2 كتابة صيغة الحدّ النوني لمتتابعة حسابية اكتب صيغة للحد النوني للمتتابعة الحسابية في كل مما يأتي: 5, -13, -31, ... (a 18- = 5 - 13- = d والحد الأول 5 الحد النوني في المتتابعة الحسابية d=-18, a₁ =5 استعمل خاصية التوزيع، ثم بسط ana+(n - 1)d a5+ (n-1)(-18) a =-18n+23 45 = 19, d = 6 (b الخطوة 1 : أوجد قيمة a الحد النوني في المتتابعة الحسابية 45 = 19, n = 5, d=6 اضرب، ثم اطرح 24 من الطرفين ana+ (n-1)d 19 = a + (5 - 1)(6) 5 = 21 الخطوة 2 كتابة الصيغة. الحد النوني في المتتابعة 5- = 4 و 6 = d استعمل خاصية التوزيع، ثم بسط aa + (n-1)d a5+ (n-1)(6) a₁ = 6n - 11 تحقق من فهمك 46 = 12, d = 8 (28) 12, 3, -6, ... (2A في بعض الأحيان يُعطى في المسألة حدان غير متتاليين في متتابعة حسابية. وتُسمّى جميع الحدود الواقعة بين قراءة الرياضيات هذين الحدّين أوساطا حسابية، ويمكنك استعمال هذا المفهوم في إيجاد الحدود المفقودة بينهما. الوسط الحسابي هو معدل عددين أو أكثر. الوسط الحسابي بين مثال 3 إيجاد الأوساط الحسابية أوجد الأوساط الحسابية في المتتابعة : 3,22 ,2 ,3 ,2 ,8 العددين a, b يساوي a + b الخطوة 1: بما أنه يوجد 4 حدود بين الحدّ الأول والحدّ الأخير؛ فإن عدد حدود المتتابعة هو الأوساط الحسابية 2 هي الحدود الواقعة بين أي حدين غير متتاليين في متتابعة حسابية. 6 = 2 + 4 إذن 6 = n . الخطوة 2: أوجد قيمة d aa+(n-1) d 228+ (61) d 30 = 5d 6 = d الحد النوني في المتتابعة الحسابية a₁ =-8, a=22, n=6 أضف 8 إلى الطرفين، ثم بسط اقسم الطرفين على 5 الخطوة 3: استعمل ل لإيجاد الأوساط الحسابية الأربعة المطلوبة. -8 -2 4 10 16 22 +6 +6 +6 +6 +6 إذن الأوساط الحسابية هي 2016 تحقق من فهمك (3) أوجد خمسة أوساط حسابية بين العددين 1836 وزارة التعليم الدرس 2-6 المتتابعات والمتسلسلات الحسابية 131 2024-1446

إرشادات للدراسة المتسلسلات الحسابية: يمكنك الحصول على المتسلسلة بوضع إشارة الجمع (+) بين حدود المتتابعة؛ لذا فالمتسلسلة الحسابية هي مجموع حدود متتابعة حسابية. ويُسمّى ناتج جمع ا الحدود 1 الأولى من المتسلسلة المجموع الجزئي، ويُرمز له بالرمز . أضف الى مطويتك مفهوم أساسي المجموع الجزئي في متسلسلة حسابية القانون ( المعادلة) المعطيات مجموع أول " حدا (5) هو: بالصيغة العامة بالصيغة البديلة a₁, an a₁,d, n S=(a+α) S₁₁ =[2a, + (n-1)d] صيغتا المجموع الجزئي في متسلسلة حسابية سُميت الصيغة S₁₁ = (a+an) بالصيغة العامة؛ لأنه تم التوصل إليها اعتمادًا على تعريف المتتابعة الحسابية، وباستعمال حدودها بشكل عام، بينما سُميت الصيغة S=12a,+(n-1)d] بالصيغة البديلة؛ لأنها تشتق من الصيغة العامة ويمكن استعمالها بديلا عن الصيغة العامة في بعض الأحيان، لابد من إيجاد إحدى القيم aa ، قبل إيجاد مجموع المتسلسلة الحسابية. وفي هذه الحالة استعمل صيغة الحد النوني. مثال 4 استعمال صيغ المجموع أوجد مجموع حدود المتسلسلة الحسابية 180 + ... + 26 + 19 + 12 الخطوة 1 7 = 12 - 19 = d ,180 = 4 ,12 = 41 يجب إيجاد قيمة " أولا كي نجد المجموع. الحد النوني في المتتابعة الحسابية a=180, a₁ = 12, d=7 ana+(n-1)d 180 12+(n - 1)(7) 168 = 7n - 7 25 = n استعمل خاصية التوزيع، ثم بسط حل المعادلة 132 الخطوة 2: استعمل إحدى الصيغتين لحساب . . تحقق من فهمك صيغة المجموع S₁₁ = [2a + (n-1)d] n = 25, a₁ = 12, d = 7 S25 = 25 [2(12) + (25 - 1)(7)] بسط S25 12.5(192) = 2400 2+4+6+ + 100 (4A n = 16, a, 240, d = 8 (4B يمكنك استعمال صيغة المجموع في إيجاد حدود المتتابعة الحسابية. مثال 5 إيجاد الحدود الثلاثة الأولى لمتتابعة حسابية أوجد الحدود الثلاثة الأولى لمتتابعة حسابية فيها 430 = a = 79, S ,7 = 41 الخطوة 1 أوجد قيمة 11 . الفصل 6 المتتابعات والمتسلسلات S=(a+a) (7+79) صيغة المجموع S₁ = 430, a₁ = 7, a,, = 79 اجمع بسط اقسم طرفي المعادلة على 43 430 = 430 = 1 (86) 430 = n(43) 10 = n وزارة التعليم Ministry of Education 2024-1446

اراشادات للدرسة
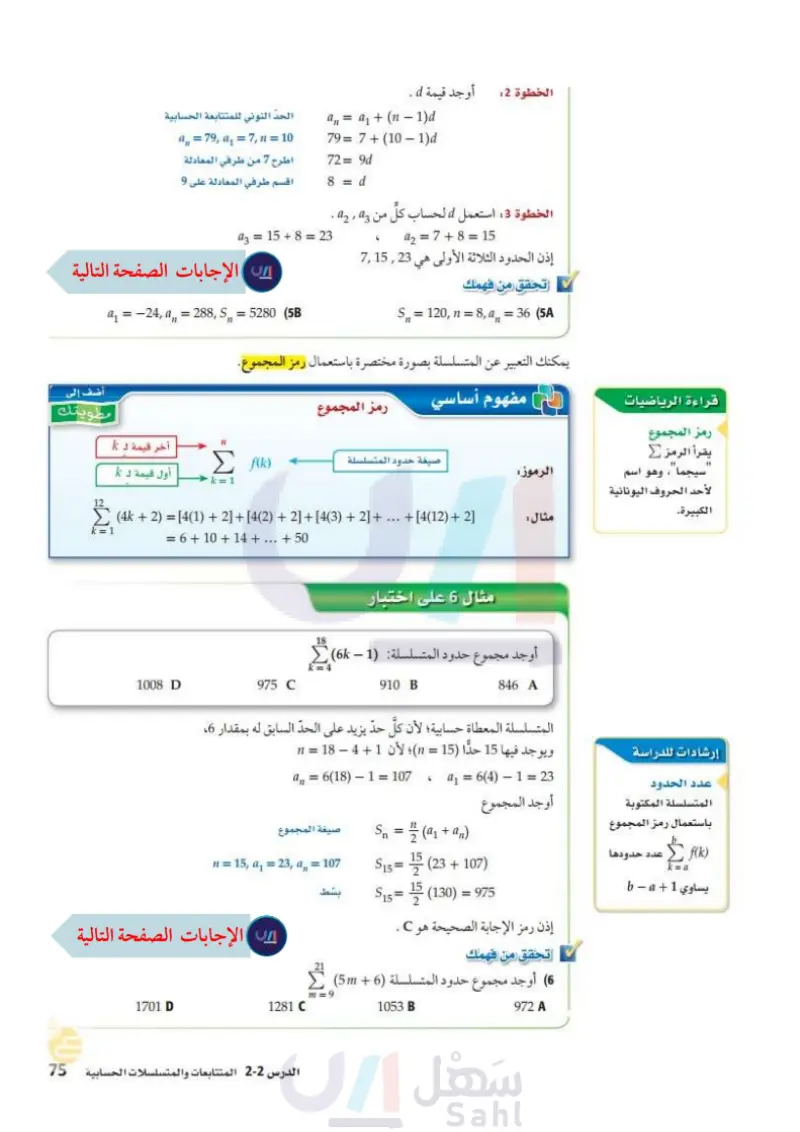
قراءة الرياضيات رمز المجموع يقرأ الرمز 2 "سيجما"، ، وهو اسم الأحد الحروف اليونانية الكبيرة. إرشادات للدراسة أوجد قيمة d . الخطوة 2 : الحد النوني للمتتابعة الحسابية a=79, a=7, n = 10 اطرح 7 من طرفي المعادلة اقسم طرفي المعادلة على 9 aa + (n-1)d 79 = 7 + (10 - 1) 72=9d 8 = d الخطوة 3: استعمل d لحساب كل من 43 ,42 . 6 42 = 7 + 8 = 15 إذن الحدود الثلاثة الأولى هي 1523 تحقق من فهمك S=120, n = 8,a,, = 36 (5A 43 = 15 + 8 = 23 a₁ =-24, a=288, S = 5280 (5B يمكنك التعبير عن المتسلسلة بصورة مختصرة باستعمال رمز المجموع الرموز مثال: مفهوم أساسي رمز المجموع صيغة حدود المتسلسلة Σ k=1 آخر قيمة لـ k أول قيمة لـ k (4k+2)= [4(1)+2]+[4(2) + 2]+[4(3) + 2]+ ... + [4(12) + 2] مثال 6 على اختبار 6+10+14 + ... + 50 أوجد مجموع حدود المتسلسلة (1) - 6 ) 846 A 910 B k=4 975 C المتسلسلة المعطاة حسابية؛ لأن كلَّ حدّ يزيد على الحد السابق له بمقدار 6، ويوجد فيها 15 حدا (15) = ) ؛ لأن 1 - 4 - 18 = n a =6(18) 1 = 107. 4 = 6(4) - 1 = 23 عدد الحدود صيغة المجموع Sn = (a + a₁) n = 15, a₁ = 23, a,, = 107 15 = 1 (23 + (107) بسط S15= 15 (130) = 975 المتسلسلة المكتوبة أوجد المجموع باستعمال رمز المجموع f(k) عدد حدودها يساوي 1 + b - a إذن رمز الإجابة الصحيحة هو C . تحقق من فهمك (6) أوجد مجموع حدود المتسلسلة (56) 972 A 1053 B 1008 D m = 9 1701 D 1281 C أضف إلى طويتك وزارة التعليم الدرس 2-6 المتتابعات والمتسلسلات الحسابية 133 2024-1446

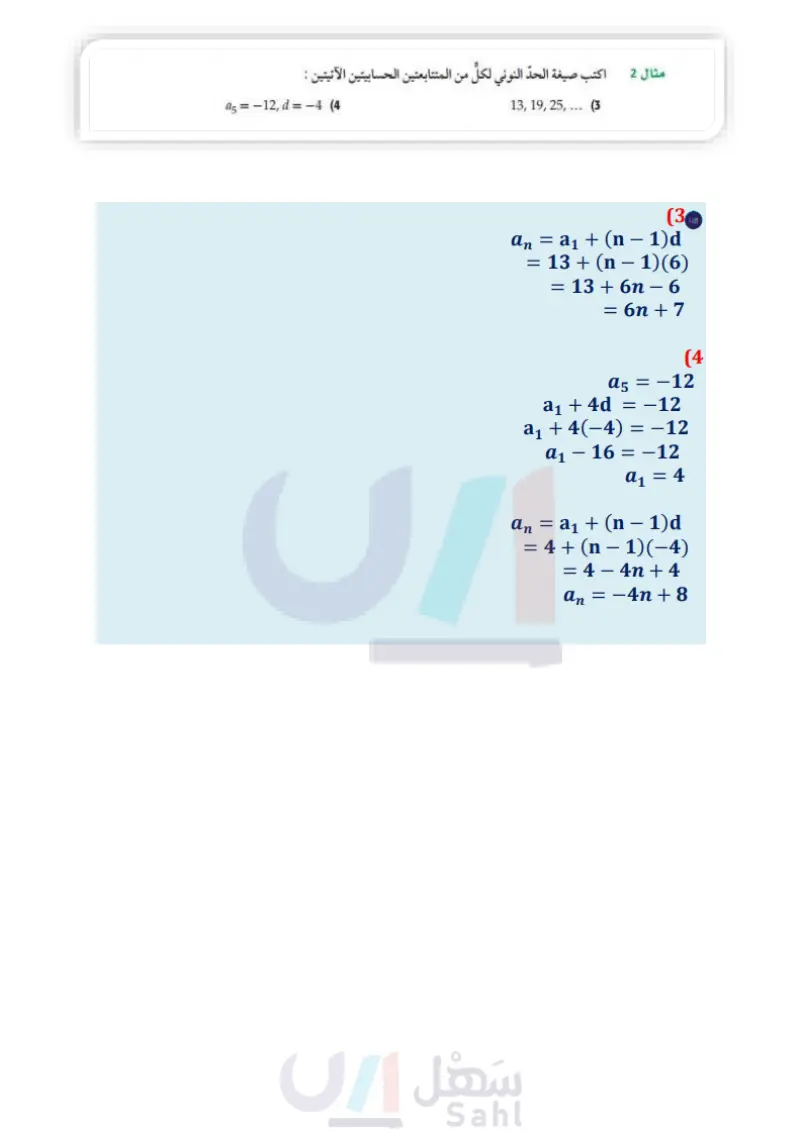
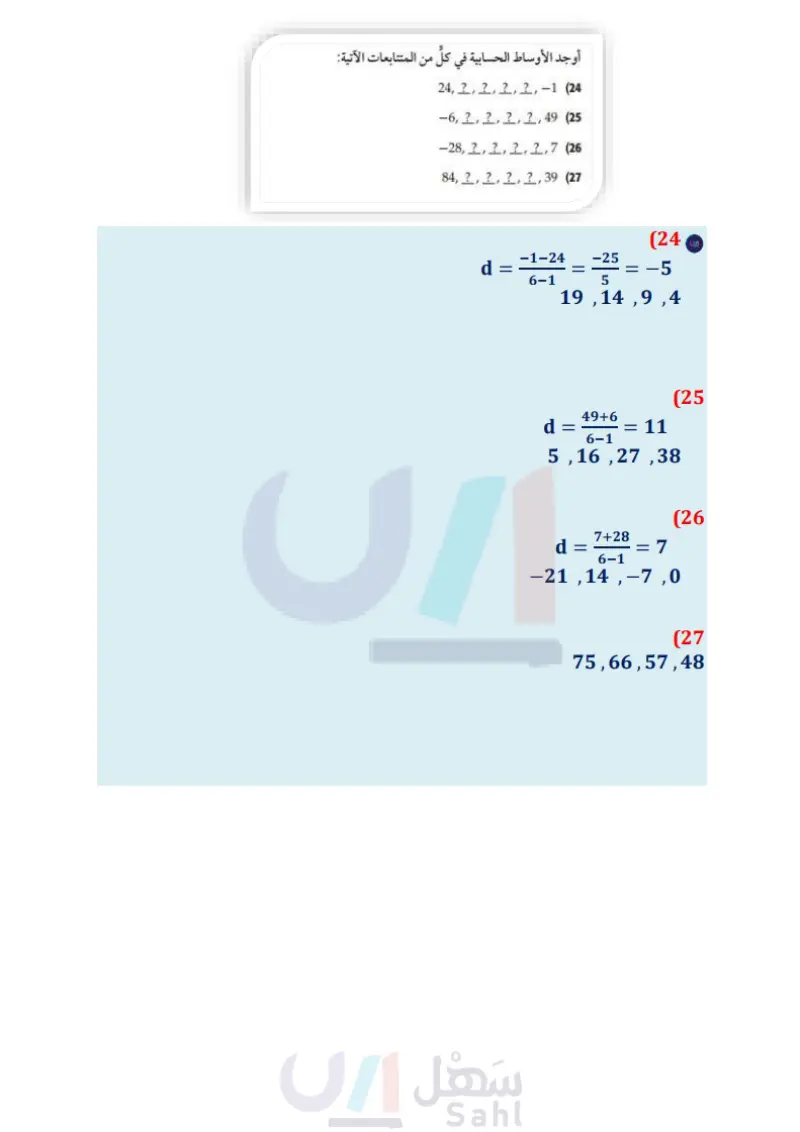
تأكد أوجد قيمة الحد المطلوب في كلُّ من المتتابعتين الحسابيتين الآتيتين : مثال 1 (1) علماً بأن : 11 = d = 9, n 14 = 4 2 18 في المتتابعة ... 1258 اكتب صيغة الحد النوني لكل من المتتابعتين الحسابيتين الآتيتين : مثال 2 13, 19, 25, (3 45 = 12, d = -4 (4) أوجد الأوساط الحسابية في كل من المتتابعتين الآتيتين: مثال 3 6,2,2,2,42 (5 أوجد مجموع حدود كل متسلسلة حسابية فيما يأتي: مثال 4 (7) أول 50 عددًا طبيعيا 4 = 12, 4, = 188, d = 4 (9 -4, ?, ?, ?,8 (6 4+8+12++200 (8) 4 = 145, d = 5, n = 21 (10 أوجد الحدود الثلاثة الأولى في كلّ من المتتابعتين الحسابيتين الآتيتين: مثال 5 41 = 8, 4, = 100, 5, = 1296 (11 n = 18, 4, = 112, S, = 1098 (12 12 13 اختيار من متعدد: أوجد مجموع حدود المتسلسلة: (9 + 3) مثال 6 k=1 تدرب وحل المسائل 134 45 A 78 B 342 C 410 D أوجد قيمة الحد المطلوب في كلّ من المتتابعات الحسابية الآتية: مثال 1 15) علما بأن : 4 = n = 66, d ,12 = 4 14) علما بأن : 16 = d = 12, n ,18- = 4 16 415 في المتتابعة ... 19-12-5 17 124 في المتتابعة ... 8.75 8.5 8.5 اكتب صيغة الحد النوني في كل متتابعة حسابية فيما يأتي: مثال 2 24, 35, 46, (18) 4 = 22, d = 9 (21) 9,2,-5,... (20 45 = 1.5, d = 4.5 (19) -12, -17,-22, ... (23 4g = -8, d = -2 (22) أوجد الأوساط الحسابية في كل من المتتابعات الآتية: مثال 3 24,2,2,2,2,-1 (24 -6,2,2,2,2,49 (25 -28, ?, ?, ?,?,7 (26 84, ?, ?, ?,?,39 (27 الفصل 6 المتتابعات والمتسلسلات وزارة التعليم Ministry of Education 2024-1446

مثال 4 أوجد مجموع حدود كل من المتسلسلات الحسابية الآتية: (28) أول 100 عدد زوجي في مجموع عة الأعداد الطبيعية. (29) أول 200 عدد فردي في مجموعة الأعداد الطبيعية. -24+ (-18)+(-12)+...+72 (31 n = 19,a=154,d=8 (33 -18+ (-15)+(-12) + ... + 66 (30 a₁ = -16,d=6, n = 24 (32 34) مسابقات ثقافية في إحدى المسابقات الثقافية تم تخصيص جوائز تصاعدية للإجابة الصحيحة عن أسئلة المسابقة، فخُصِّص للسؤال الأول 100 ريال، وتزيد قيمة الجائزة 50 ريالًا للسؤال التالي، وهكذا. إذا شارك سعد في المسابقة، وأجاب عن 11 سؤالا بصورة صحيحة، فما مجموع مبلغ الجائزة الذي يستحقه؟ مثال 5 أوجد الحدود الثلاثة الأولى في كلّ من المتتابعات الحسابية الآتية: a₁ =3,a=66, S = 759 (36 41 = - 33, n = 36,5 = 6372 (38) 13 k=4 12 (4k+1) (40 (-3k+2) (42 k=0 a₁ =48, a = 180,S,, = 1368 (35 n = 28,a,, = 228, S₁ = 2982 (37 مثال 6 أوجد مجموع حدود - ود كل من المتسلسلات الآتية: 16 Σ (4k-2) (39 k=1 16 Σ(2k+6) (41 k=5 الربط بالحياة يجب على الإنسان أن يكتب عقدا (43) قرض حسن: اقترض عليّ مبلغًا من المال من أحد أصدقائه، واتفقا على أن يقوم بتسديده مقسطا كما يأتي: القسط الأول 50 ريالا، وكل قسط تال يزيد على القسط السابق بمقدار 25 ريالا. فإذا علمت أن عدد الأقساط هو 12 فما قيمة القرض؟ استعمل المعلومات المعطاة في كلّ من الأسئلة الآتية؛ لكتابة معادلة تُمثل الحد النوني لكل متتابعة حسابية: 44) الحد رقم 100 في المتتابعة يساوي 245، وأساس المتتابعة يساوي .13 . بينه وبين من يقرضه المال عملا بقوله تعالى في سورة (45) الحد الحادي عشر في المتتابعة يساوي 78 ، وأساس المتتابعة يساوي 9 . البقرة: تَأَيُّهَا الَّذِينَ ءَامَنُوا إِذَا تَدَايَنتُم بِدَيْنِ إِلَى أَجَلٍ مُّسَمًّى (46) الحد الخامس والعشرون في المتتابعة يساوي ،121، والحد الثمانون يساوي 506 . (47) تنظيم تُصفّ الطاولات المستطيلة الشكل في قاعات الاحتفالات متجاورة لتشكّل طاولة كبيرة. ويُبيِّنُ الشكل المجاور عدد الأشخاص الذين يمكن توزيعهم على التشكيلين الأول والثاني من الطاولات. a) ارسم شكلا يُبين عدد الأشخاص على الطاولات في كل من الحدود الثلاثة التالية (بإضافة طاولة كلّ مرَّة). اكتب معادلة تُمثل الحد النوني في هذا النمط. هل من الممكن ترتيب الطاولات بهذه الطريقة، بحيث يستطيع 100 شخص الجلوس؟ وضح وزارة التعليم الدرس 2- المتتابعات والمتسلسلات الحسابية 135 2024-1446 إجابتك.

الربط مع الحياة
الربط بالحياة رياضة الجري تفيد في إنقاص الوزن وتقوية المفاصل والعضلات، وتحسين عمل 48) جاذبية: عندما يسقط جسم سقوطا حرا تحت تأثير الجاذبية الأرضية ومع إهمال مقاومة الهواء، فإنه يقطع مسافة 16 قدما في الثانية الأولى، و 48 قدما إضافية في الثانية الثانية ، و 80 قدما إضافية في الثانية الثالثة، وهكذا . ما المسافة التي يقطعها هذا الجسم في 10 ثوان؟ 49) دخل سنوي: إذا كان الدخل السنوي لمؤسسة في السنة الأولى 92000 ريال، ويزيد سنويا بمقدار 16000 ريال، ففي ا أي سنة يـ يصبح دخلها 380000 ريال ؟ (50) رياضة خلال استعداده لأحد سباقات الجري لمسافات طويلة، يُخطّط فيصل للتدرب على الجري لمسافة 3 أميال يوميًا في الأسبوع الأول، ومن ثَمَّ يقوم بزيادة المسافة بمقدار نصف ميل أسبوعيا. اكتب معادلة للحد النوني لهذه المتتابعة. ) إذا استمر فيصل بالتدرب على هذا النمط، ففي أي أسبوع يصل إلى قطع مسافة 10 أميال يوميا؟ هل يُعد الاستمرار على هذا النمط إلى ما لا نهاية منطقياً؟ وضح إجابتك. 11 51) تمثيلات متعددة : معتبرا (2 + 2) أجب عما يأتي: القلب والأوعية الدموية k=1 والتخلص من الإرهاق والتوتر a جدوليا : اعمل جدولًا للمجاميع الجزئية للمتسلسلة، حيث 10 ≥ k > 1 . ورفع مستوى اللياقة البدنية والصحة العامة. ) بيانيًا مثل بيانيا المجاميع الجزئية التي أوجدتها في الفرع a ، وذلك بتمثيل النقاط ( ) . بيانيا : مثل الدالة f(x) = x 2 + 3x بيانيا على المستوى الإحداثي نفسه، حيث 10 ≥ x ≥ 0 d لفظيا : ماذا تلاحظ حول التمثيلين البيانيين؟ e) تحليليا : ماذا تستنتج حول العلاقة بين التمثيل البياني للدالة التربيعية والتمثيل البياني لمجموع المتسلسلة الحسابية؟ جبريًا أوجد المتسلسلة الحسابية التي يكون فيها التمثيل البياني للمجاميع الجزئية (k, S) هو نفسه للدالة x) = x 2 + x) أوجد قيمة x في كل مما يأتي: (8k+2)=1032 (53 k=5 k=3 (6k-5) 928 (52 مسائل مهارات التفكـ لعليا (54) تبرير: إذا كان هو الحد الثالث في متتابعة حسابية ، و هو الحد الخامس، و هو الحد الحادي عشر، فعبر عن ، بدلالة a, b . (55) تحد : يوجد ثلاثة أوساط حسابية بين العددين a, b في متتابعة حسابية. إذا كان الوسط الحسابي للأوساط الثلاثة 16 ، فأوجد الوسط الحسابي للعددين ab (56) مسألة مفتوحة : اكتب متسلسلة حسابية فيها 8 حدود و مجموعها .324 وزارة التعليم Ministry of Education 2024-1446 الفصل 6 المتتابعات والمتسلسلات 136

رياضة الجرى تفيد في انقاص الوزن وتقوية المفاصل والعضلات وتحسين عمل القلب والاوعية الدموية
تدريب على اختبار (57) اكتب بين أوجه الشبه وأوجه الاختلاف بين المتتابعات الحسابية والمتسلسلات الحسابية. 58 صيغ: اشتق صيغة الحد النوني للمتتابعة الحسابية. (59) صيغ اشتق قاعدة لإيجاد مجموع المتسلسلة الحسابية، بحيث لا تحتوي على 91. (60) صيغ اشتق الصيغة البديلة لإيجاد مجموع المتسلسلة الحسابية باستعمال الصيغة العامة للمجموع. (61) تحد بالعودة إلى فقرة "لماذا ؟" ما الطريقة التي استعملها كارل جاوس في إيجاد مجموع ا الأعداد الصحيحة من 1 إلى 100؟ يمكنك البحث في الإنترنت). (62) تُشكل قياسات زوايا المثلث أدناه متتابعة حسابية. إذا كان (63) العبارة 3 + 2 + 1 تكافئ: قياس الزاوية الصغرى ،36 ، فما قياس الزاوية الكبرى؟ k = 1 IM IM~ k-k C k=1 3 k=1 IM 36° ΣΑΒ 90° C 75° A 97° D 84° B مراجعة تراكمية حدد ما إذا كانت كلٌّ من المتتابعات الآتية حسابية أم لا. أجب "بنعم" أو "لا" : (الدرس 1-6) -6, 4, 14, 24, ... (64 2 741 '5'5'5' (65 10,8,5,1, (66 67 فيزياء: ترتبط المسافة التي يستطيل فيها الزنبرك بالكتلة المعلّقة فيه. ويعبر عن هذه العلاقة بالقاعدة d = km ، حيث d المسافة، و الكتلة، و ثابت الزنبرك. وعند وصل زنبركين لهما الثابتان على التوالي، فإن ثابت الزنبرك ( الناتج ، يُحسب باستعمال المعادلة 1 1 k 1 + الدرس (56) إذا وصل زنبركان على التوالي، وكان ثابت الزنبرك الأول 12cm/g، وثابت الزنبرك الثاني 8/8cm ، فأوجد ثابت الزنبرك الناتج. إذا عُلّقت كتلة مقدارها 5 جرامات (كما في الشكل ) فما مقدار استطالة الزنبركين؟ أوجد قيمة كل مما يأتي: (مهارة سابقة) 2.36 (68 (69 الزنبرك 1 الزنبرك 1 الزنبرك 2 (-1)* (70 wwwwwwwww-wwwwwwww k, = 12 cm / g الزنبرك 2 k, = 8 cm / g وزارة التعليم الدرس 2- المتتابعات والمتسلسلات الحسابية 137 2024-1446